Príklad 2.3.1: Pôsobisko sily  sa posúva po krivke . Vypočítajte prácu sily v časovom intervale t₁ = 1 s, t₂ = 3 s.

Riešenie: Zo zadania príkladu vyplýva že sila nie je konštantná (mení sa s časom) a jej smer sa mení vzhľadom ku posunutiu (pohyb po krivke). Pri výpočte práce použijeme definičný vzťah
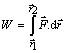(1).


Na to, aby sme vedeli prácu vypočítať potrebujeme vedieť posunutie , ktoré v našom prípade nie je známe, poznáme len . Elementárne posunutievyjadríme pomocou. Po dosadení a úprave dostaneme
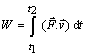 (2), 

kde . Dosadením za a do vzťahu (2) pre prácu
  (3)

Sila vykoná prácu 144 J v danom časovom intervale.

Späť

Príklad 2.3.2: Akú prácu treba vykonať pri stlačení nárazníkovej pru­žiny vagóna o x₀ = 5 cm, keď na jej stlačenie o x₁ = 1 cm  treba silu F₁ = 3.10⁴ N a keď platí, že sila je priamo úmerná  skráteniu pružiny?

Riešenie: Zo zadania príkladu vyplýva, že sila je priamoúmerná skráteniu pružiny, čo matematicky vyjadruje F = kx. Sila mení svoju veľkosť, ale pôsobí v smere skrátenia pružiny, na výpočet práce potrebnej na stlačenie nárazníkovej pružiny vagóna použijeme
.

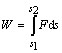V našom prípade ds = dx, s₁ = 0, s₂ = x₀ a F = kx. Potom po dosadení
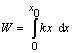    (1)

a úpravou práca
      (2).


Konštantu k nepoznáme, ale z počiatočných podmienok príkladu (na skrátenie o x₀ = 5 cm treba silu F₁ = 3.10⁴ N, čo zapíšeme F₁ = kx₁), pre k vyplýva
    (3).

Dosadením (3) do (2) práca

Pri stlačení nárazníkovej pružiny o 5 cm treba vykonať prácu 3750 J.

Späť

Príklad 2.3.3: Strela hmotnosti 20 g zasiahne rýchlosťou 400 ms^-1 strom. Do akej hĺbky prenikne, ak priemerný odpor dreva je F = 9000 N?

Riešenie: Zaujíma nás ako hlboko prenikne strela do stromu, teda nás zaujíma dráha, na ktorej strela zastaví. Na teleso pôsobí sila po dráhe, sila koná prácu, dôsledkom ktorej sa mení rýchlosť strely, teda sa mení jej kinetická energia. Potom na výpočet dráhy použijeme vzťah
W = D E_k
W = E_k2 - E_k1    (1)

kde E_k1 - kinetická energia na začiatku pohybu, E_k2 - kinetická energia na konci pohybu.

Prácu koná stála sila v opačnom smere ku dráhe, prácu môžeme vyjadriť pomocou vzťahu (2.3.5), kde sila F bude mať opačné znamienko

W = - F s .          (2)

Dosadením (2) do (1)

- F s = E_k2 - E_k1

kde
.

 Pohyb strely sa vplyvom odporovej sily zastaví, preto jej rýchlosť na konci pohybu bude nulová. Potom aj E_k2 = 0.

Úpravou





  Strela prenikne do hĺbky 18 cm.

Späť

Príklad 2.3.4: Vypočítajte okamžitý výkon sily v čase 3 s z príkladu 2.3.1, ak pôsobisko sily sa posúva po krivke .

Riešenie: 1. spôsob
Okamžitý výkon je definovaný vzťahom



V príklade 2.3.1 sme vypočítali závislosť práce od času  . Potom okamžitý výkon
 


a v čase t = 3 s  P = 128 W.


Okamžitý výkon sily v čase 3 sekundy je 128 W.

2. spôsob:
Pri výpočte okamžitého výkonu môžeme vychádzať aj zo vzťahu  (1).

V príklade 2.3.1 sme vypočítali rýchlosť
, pričom sila je daná .

Potom dosadením do vzťahu (1) , čo je rovnaký tvar ako pri počítaní výkonu pri 1. spôsobe. Ďalej postupujeme rovnako ako v prvom prípade.

Späť

Príklad 2.3.5: Na časticu hmotnosti 0,02 kg pôsobí sila veľkosti  F = 0,6 t (N). Vypočítajte hodnotu impulzu sily a veľkosť rýchlosti telesa v čase 2 s, ak na začiatku bolo teleso v pokoji a smer rýchlosti bol rovnaký ako smer pôsobiacej sily.

Riešenie: Poznáme hmotnosť častice, jej počiatočnú rýchlosť v₁ = 0 a veľkosť pôsobiacej sily, ktorá sa mení s časom. Na výpočet impulzu použijeme vzťah (2.3.13), ktorého veľkosť
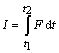            (1)

dosadením za silu do (1)

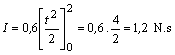
Veľkosť impulzu sily je 1,2 N.s.

Na výpočet veľkosti rýchlosti telesa v čase 2 s použijeme vzťah (2.3.15), pretože hybnosť telesa súvisí s jeho rýchlosťou. Zo zadania vyplýva, že teleso sa bude pohybovať v smere sily preto tento vzťah upravíme
   (2)

kde p₁ je hybnosť častice v čase t₁ = 0 s, p₂ je hybnosť častice v čase t₂ = 2 s. Hybnosť častice p₂ = m v₂ a p₁ = m v₁ = 0. Dosadením do (2)
m v₂ - 0 = I

Veľkosť rýchlosť častice v čase 2 s je 60 m/s.

Späť

Príklad 2.3.6: Stála sila F pôsobí na teleso tiaže G. Za akú dobu sa pritom zväčší rýchlosť telesa na n-násobok pôvodnej rýchlosti v₀, ktorou sa teleso vyznačovalo v okamihu, keď sila začala naň pôsobiť?

Riešenie: Označme čas, v ktorom má teleso rýchlosť v = nv₀ (1), pričom v₀ je počiatočná rýchlosť. Zaujíma nás doba, počas ktorej pôsobí sila na teleso, teda časový účinok sily - impulz. Sila je stála, potom pre vyjadrenie impulzu použijeme vzťah (2.3.14) v skalárnom tvare I = FDt (2) (predpokladáme, že smer pôsobiacej sily je rovnaký ako smer rýchlosti telesa). Časový interval Dt = t - t₀ (3), kde t₀ = 0 s je čas na začiatku pôsobenia sily na teleso. Pôsobením sily dôjde k zväčšeniu rýchlosti z v₀ na v, resp. zmene hybnosti z p₀ na p. Dôsledkom impulzu sily I = Dp = p - p₀ (4), kde p₀ je hybnosť telesa na začiatku v čase t₀ a p je  hybnosť telesa v čase t. 
Použitím vzťahov (2) a (4)
 
FDt = Dp = p - p₀   (5)

a dosadením (3) do (5)

F(t - t₀) =  p - p₀

úpravou
(6)

Na vyjadrenie p a p₀ použijeme vzťah (2.1.1) v skalárnom tvare (p, p₀ majú rovnaký smer ako v, v₀), p = mv  (7) a p₀ = mv₀ (8). Použitím vzťahov (6), (7) a (8) 


pričom hmotnosť vyjadríme zo vzťahu pre tiaž (2.4.2.)
,

potom
   (9)


Dosadením (1) do (9) za rýchlosť v a úpravou
     (10)

Doba, za ktorú sa zväčší rýchlosť telesa na n-násobok je daná vzťahom (10).

Späť


Príklad 2.3.7: Basedbalová loptička hmotnosti 140 g letí tesne pred odpálením vodorovne rýchlosťou 39 m/s. Nenarazí na pálku kolmo, ale sa od nej odrazí pod uhlom 30 stupňov rýchlosťou 45 m/s. Vypočítajte priemernú silu, ktorou pálka na loptičku pôsobila, ak zrážka prebehla za 1,2 ms. 

Riešenie: Označme rýchlosť loptičky pred odpálením v₁ = 39 m/s, po odpálení v₂ = 45 m/s a silu, ktorú chceme vypočítať , uhol pod ktorým sa loptička odrazila a = 30⁰ a jej hmotnosť m = 140 g. Doba zrážky loptičky s pálkou je Dt = 1,2 ms. Na výpočet premennej sily použijeme vzťah (2.3.16) (ide o nárazovú silu), ktorý pre naše účely napíšeme v tvare ,
odtiaľ
  (1). 


Aby sme mohli vypočítať premennú silu, musíme vedieť hodnotu impulzu a doby, za ktorú zrážka nastala. 

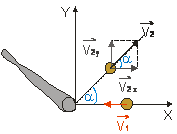
Obr. 2.3.13

V našom prípade je impulz daný vektorovým tvarom , pretože sa mení smer rýchlosti resp. hybnosti po zrážke. 
Veľkosť impulzu (2)


a na jej výpočet musíme vedieť veľkosti jeho jednotlivých zložiek impulzu:
 

, kde .

Podľa obr. 2.3.10  vzhľadom na zvolený súradnicový systém: v_1x = -v₁, v_1y = 0, v_2x = v₂cos a, v_2x = v₂sin a. Potom pre veľkosť zložiek impulzu: 
I_x = p_2x - p_1x = mv_2x - mv_1x= mv₂cos a + mv₁   (3) 
I_y = p_2y - p_1y = mv_2y - mv_1y= mv₂sin a + m.0      (4).

Dosadením (3), (4) do (2)
(5) 

a pre priemernú silu

  .



Použitím číselných hodnôt 

Priemerná sila, ktorou pálka pôsobila na loptičku pri zrážke je približne 9500 N.  

Späť 

Príklad 2.3.8: Dokážte, že tiažové pole Zeme je konzervatívne silové pole.

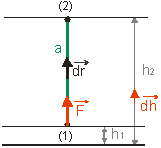
Riešenie: Pri dokazovaní budeme predpokladať, že premiestňujeme guľôčku o hmotnosti m v gravitačnom poli po dvoch rôznych cestách (obr. 2.3.11) z bodu (1) do bodu (2). Označme h₁ výšku bodu (1) a h₂ výšku bodu (2) vzhľadom na zemský povrch. 

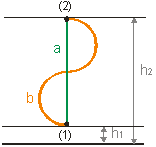
Obr. 2.3.14

Silu, ktorou premiestňujeme guľôčku označme F´ a smer jej posunutia po dráhe je daný elementárnym posunutím . Vypočítame akú prácu vykoná sila pri premiestňovaní guľôčky po oboch dráhach. Smer posunu z bodu (1) do bodu (2) udáva .

Dráha a - zelená dráha

Na výpočet práce použijeme vzťah (2.3.19)

Obr. 2.3.15

V tomto prípad má sila rovnaký smer ako elementárne posunutie a poloha prvého (druhého) bodu je daná  h₁, ( h₂).Využitím týchto podmienok(obr. 2.3.12) potom práca 


kde a cos a = cos 0⁰ = 1.

Potom

Dráha b - oranžová dráha    

 
Použijeme opäť vzťah (2.3.19) na výpočet práce



v tomto prípade sa pôsobisko sily pohybuje po krivke, teda poloha sa stále mení. Jej smer budeme popisovať vzhľadom na vektor , ktorý určuje posunutie z bodu (1) do (2) v horizontálnom smere (obr. 2.3.13a). Potom pre dr a dh platí vzťah (obr. 2.3.13b) odkiaľ dh = dr cos a.   

 

Potom použitím vzťahu
 



Práca W₁ = W₂, gravitačné pole je konzervatívne.

Späť  

Príklad 2.3.9: Pomocou predchádzajúceho príkladu odvoďte potenciálnu energiu tiažového poľa v malej výške nad povrchom Zeme.

Riešenie: Predpokladajme, že výšky bodov (1) a (2), ktoré sme označili h₁  a h₂ z predchádzajúceho príkladu sú oproti polomeru Zeme oveľa menšie. Vonkajšia sila , ktorou premiestňujeme teleso z bodu (1) do bodu (2) prekonáva tiažovú silu . Pre veľkosť vonkajšej sily potom platí F´ = mg. Dosadením výsledku pre prácu vonkajšej sily z predchádzajúceho príkladu

W = F´(h₂ - h₁) = mg(h₂ - h₁) = mgh₂ -mgh_1. 

Ak   h₁ = 0 potom pre teleso hmotnosti m nachádzajúce sa v nie veľkej výške h nad zemským povrchom v tiažovom poli Zeme platí, že E_p = mgh  (*).


Potenciálna energia tiažového poľa v malej výške nad povrchom Zeme je daná vzťahom E_p = mgh.

Späť

Príklad 2.3.10: Do nádrže, ktorá je vo výške 18 m, treba nečerpať za 5 hodín 1000 hl vody. Aký výkon musí mať motor čerpadla? 

Riešenie: Výkon motora je daný vzťahom (2.3.10)
(1)


kde t = 5 h. Prácu koná čerpadlo, ktoré premiestňuje vodu do výšky h = 18 m, teda spôsobuje zmenu polohy vody. Použitím vzťahu (2.3.21), pre prácu čerpadla platí W = DE_p= E_p1- E_p0, kde E_p0 je potenciálna energia na povrchu Zeme, (ktorej hodnotu si volíme za nulovú E_p0 = 0), E_p1 je potenciálna energia vo výške h. Použitím vzťahu (*) z predchádzajúceho príkladu pre E_p, potom práca W = mgh - 0 (2). Dosadením (2) do (1) 

kde m = rV potom
  .

Dosadením číselných hodnôt
.

Výkon motora musí byť 981 W, aby načerpal do výšky 18 m 1000 hl vody.

Späť

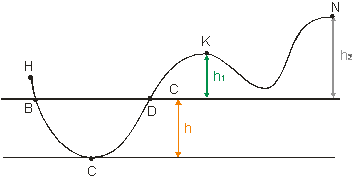
Príklad 2.3.11: Nech hmotný bod vykonáva pohyb po krivke ako je to na obr. 2.3. 14. a) Aká bude jeho rýchlosť v bode C, ak je vypustený z bodu B, kde v_B = 0 m/s? b) Akú rýchlosť máme udeliť hmotnému bodu v bode B, aby pri svojom pohybe dosiahol bod K?  

Riešenie: Pri výpočte použijeme zákon zachovania mechanickej energie, podľa ktorého je súčet kinetickej a potenciálnej energie v každom bode konzervatívneho silového poľa konštantný a rovný celkovej mechanickej energii.
a) Zaujíma nás rýchlosť bodu v bode C, ktorý bol vypustený z bodu B, teda budeme popisovať celkovú mechanickú energiu vzhľadom na tieto dva body (B a C). Kinetická energia závisí od rýchlosti a je daná vzťahom a potenciálne energia závisí od výšky E_p = mgh. Zvoľme za nulovú potenciálnu hladinu, hladinu ktorá prechádza bodom C (E_pC = 0).



bod B: rýchlosť je v_B = 0, teda E_kB = 0 (1), vzhľadom na E_pC = 0 je poloha bodu B vo výške h, teda E_pB = mgh (2). Celková mechanická energia E_B = E_kB + E_pB (3).

bod C:  rýchlosť označme v_C, teda (4) a potenciálna energia je E_pC = 0 (5). Celková mechanická energia E_C = E_kC + E_pC (6).


Zo zákona zachovania mechanickej energie vyplýva, že 

E_B = E_C = konšt. (7).

  

Obr.2.3.17

Dosadením (3) a (6) do (7)

E_Bk + E_Bp = E_kC + E_pC .

Využitím (1), (2), (4) a (5) potom rovnicu prepíšeme na tvar
 



odtiaľ pre rýchlosť v bode C
     (*) .

Rýchlosť v bode C je daná vzťahom (*).

Keďže predpokladáme pohyb v poli konzervatívnych síl (bez trenia) bod sa bude stále pohybovať medzi bodmi B a D, aby sa dostal vyššie nad bod D (výšku h) musíme mu udeliť v bode B rýchlosť.

b) Teraz nás zaujíma rýchlosť v bode B, ktorú máme udeliť bodu, aby dosiahol bod K. Teda budme určovať celkovú mechanickú energiu vzhľadom na body (B a K).

bod B: rýchlosť v_B nie je nulová, teda (7), vzhľadom na E_pC = 0 (8) je poloha bodu B vo výške h, teda E_pB = mgh (9). celková mechanická energia E_B = E_kB + E_pB (10). 

bod K: bod sa nachádza vzhľadom na E_pC = 0 vo výške h + h₁, potom E_pK = mg(h + h₁) (11), rýchlosť bodu v K je v_K = 0 (dosiahne bod K, zastaví sa ),  E_kK = 0 (13). Celková mechanická energia E_K = E_kK + E_pK (14).

Zo zákona zachovania mechanickej energie 

E_B = E_K = konšt. (15).

Dosadením (10) a (14) do (15)

E_kB + E_pB = E_kK + E_pK .

Využitím (7), (9), (11) a (13)


odtiaľ pre rýchlosť
(**)

Aby hmotný bod pri svojom pohybe dosiahol bod K, treba mu udeliť v bode B rýchlosť, ktorá je daná vzťahom (**).

Ak by sme chceli, aby sa hmotný bod dostal do vyššej výšky musíme mu udeliť väčšiu rýchlosť ako je daná vzťahom (**). 

Späť

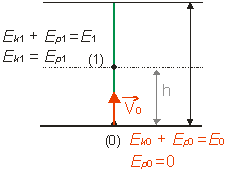
Príklad 2.3.12: Teleso bolo vyhodené zvisle nahor rýchlosťou 20 ms^-1. V akej výške sa jeho kinetická energia rovná potenciálnej?

Riešenie: Zaujíma nás v akej výške h bude E_k1  =  E_p1 (1). Pri výpočte použijeme zákon zachovania mechanickej energie pomocou, ktorého vyjadríme celkovú mechanickú energiu v bode na začiatku pohybu, označme ho (0) a v bode (1) vo výške h. Za nulovú potenciálnu hladinu zvolíme hladinu prechádzajúcu povrchom Zeme E_p0 = 0. Kinetická energia závisí od rýchlosti, so zvyšujúcou výškou h sa zmenšuje. Potenciálna energia závisí od výšky a vzhľadom na nulovú potenciálnu hladinu sa so zväčšujúcou výškou zväčšuje (obr. 2.3.). 

Obr. 2.3.18

V bode 0 je   (2)   E_p0 = 0 (3) a celková mechanická energia E₀ = E_k0 + E_p0 (4). V bode 1 označme kinetickú energiu E_k1 a potenciálnu energiu E_p1 = mgh (5), celková


energia je E₁ = E_k1 + E_p1 (6).

Podľa zákona zachovania mechanickej energie 

E₀  =  E₁ (7). 

Použitím (4) a (6) 

E_k0 + E_p0 = E_k1 + E₁ (8)

Ak do (8) dosadíme (2), (3), (1) a (5)



odtiaľ pre h   
  (9)



dosadením číselných hodnôt 



Vo výške 10,19 m bude potenciálna energia rovnaká ako kinetická. 

Späť