| 2.3 Hodnotenie účinkov sily a energia | Potenciálna energia hmotného bodu 7/9 |
Potenciálna energia hmotného bodu
V tejto časti si ukážeme ako vypočítať prácu v prípade, keď chceme
zo zemského povrchu dvihnúť teleso do určitej výšky,
keď chceme zmeniť polohu telesa zaveseného na pružine alebo odtiahnuť kovový
predmet od tyčového magnetu či na vodič nabitý záporným nábojom chceme umiestniť ďalší záporný
náboj.
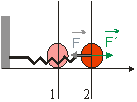
Majme guľôčku (hmotný bod) pripevnenú na koniec pružiny a ťahom ruky ju premiestnime z polohy 1 do polohy 2 po dráhe s (obr. 2.3.10).

Obr.2.3.10: Guľôčka je premiestnená z polohy (1) do (2) ťahom ruky.
V tomto prípade koná prácu vonkajšia sila (sila ktorou naťahujeme
pružinu)![]()
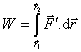 . (2.3.22)
. (2.3.22)
V oboch krajných polohách má guľôčka nulovú kinetickú energiu (jej rýchlosť
je nulová), aj napriek tomu, že sme vykonali prácu. To je možné v súlade s
prvým Newtonovým pohybovým zákonom len tak, že existuje sila (pružná sila
pružiny)
![]() ,
pre ktorú platí
,
pre ktorú platí
![]() .
(2.3.23)
.
(2.3.23)
Práca vonkajšej sily sa prejaví v tom, že hmotný bod sa premiestnil z polohy 1 do polohy 2
(pružina je natiahnutá). Keď pružinu uvoľníme, vráti sa guľôčka do počiatočnej
polohy 1. Napätá pružina má schopnosť konať prácu, čo sa prejaví pri
premiestnení hmotného bodu z miesta 2 do miesta 1. Vonkajšia sila
prekonávala silu pružnosti.
 |
V prípadoch uvedených na začiatku vonkajšia
sila pri konaní práce prekonáva tiažovú silu pri premiestnení telesa
zo zemského povrchu, magnetickú silu pri odťahovaní kovového predmetu
od magnetu a elektrickú silu pri umiestňovaní záporného náboja na
nabitý vodič. |
Celková práca síl pôsobiacich na hmotný bod je v tomto prípade
nulová, ale prácou vonkajšej sily hmotný bod upevnený na pružine získal schopnosť
konať prácu, teda má určitú formu energie, aj v prípade, že je v kľude.
Túto energiu nazývame potenciálna energia.
Potenciálnu energiu možno definovať len v poli konzervatívnych (potenciálových)
síl. Sila je konzervatívna, ak závisí iba od polohy a práca vykonaná
touto silou závisí iba o počiatočného a koncového bodu dráhy, pozdĺž
ktorej sila pôsobí na hmotný bod, práca teda nezávisí od dĺžky prejdenej
dráhy. To znamená, že práca vykonaná pozdĺž uzavretej dráhy je nulová.
Príklad 2.3.8
Je treba si uvedomiť, že na rozdiel od kinetickej energie,
potenciálna energia hmotného bodu závisí nielen od charakteristík hmotného
bodu, ale aj od vlastností silového poľa. preto sa pre potenciálnu energiu
nedá určiť jediný výraz ako pre kinetickú
energiu.
Zmena potenciálnej
energie
Pomocou práce vykonanej pri premiestnení hmotného bodu v konzervatívnom
silovom poli definujeme zmenu potenciálnej
(polohovej) energie hmotného bodu v uvažovanom silovom poli.
Nech Ep1 je potenciálna energia hmotného bodu v
mieste1 a Ep2 je potenciálna energia hmotného bodu
v mieste 2. Zmenu potenciálnej energie DEp
= Ep2 -Ep1 definujeme pomocou práce, ktorú vykonajú vonkajšie sily pri premiestnení
hmotného bodu z polohy l do polohy 2. So zreteľom na vzťah
pre prácu (3.2.22) a zohľadnením vzťahu
(2.3.23), môžeme zmenu potenciálnej energie definovať aj vzťahom
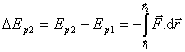 .
(2.3.24)
.
(2.3.24)
alebo
DEp = Ep2 -Ep1 = W (2.3.25)
Vektory
![]() a
a
![]() v rov. (2.3.24) určujú polohu bodov 1 a 2 a
v rov. (2.3.24) určujú polohu bodov 1 a 2 a![]() je sila, ktorou na hmotný bod
pôsobí konzervatívne silové pole. Podľa uvedenej definície predstavuje
zmena potenciálnej energie prácu vonkajších síl potrebnú na premiestnenie
telesa medzi dvoma polohami za neustálej rovnováhy vonkajšej sily a sily poľa.
je sila, ktorou na hmotný bod
pôsobí konzervatívne silové pole. Podľa uvedenej definície predstavuje
zmena potenciálnej energie prácu vonkajších síl potrebnú na premiestnenie
telesa medzi dvoma polohami za neustálej rovnováhy vonkajšej sily a sily poľa.
 |
Zo vzťahu (2.3.25) vyplýva, že môžeme len
určiť zmenu potenciálnej energie a ak chceme hovoriť o potenciálnej
energii v danom mieste musíme si zvoliť jej hodnotu v jednom bode.
Potenciálna energia je určená s presnosťou na ľubovoľnú aditívnu
konštantu. |
Pozri ešte: Závislosť sily od
potenciálnej energie hmotného bodu