| 2.3 Hodnotenie účinkov sily a energia | Zákon zachovania mechanickej energie 8/9 |
Zákon zachovania mechanickej energie
Uvažujme o dynamický izolovanom systéme, o ktorom predpokladáme, že na
hmotný bod okrem sily konzervatívneho poľa nepôsobí žiadna iná sila.
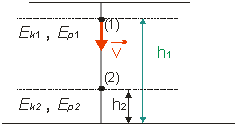
Vplyvom silového poľa sa môže zmeniť poloha hmotného bodu a aj jeho
pohybový stav, tak ako je to napr. pri voľnom páde telesa v poli zemskej tiaže
(obr.2.3.11).

Obr. 2.3.11: Pri voľnom páde telesa v poli zemskej tiaže sa vplyvom silového poľa mení poloha hmotného bodu a aj jeho pohybový stav.
Práca, ktorú pole vykoná pri premiestnení hmotného bodu z polohy 1 do
polohy 2 je rovná rozdielu kinetickej energie v týchto bodoch (rovnica (2.3.7)), preto môžeme pre písať
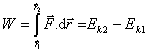 (2.3.29).
(2.3.29).
Podľa rov. (2.3.24) zmena potenciálnej energie pri diskutovanom premiestnení
hmotného bodu taktiež súvisí s prácou vykonanou silovým poľom.
Porovnaním vzťahov (2.3.24) a (2.3.29) dostaneme rovnicu
![]() (2.3.30) ,
(2.3.30) ,
ktorá hovorí, že súčet kinetickej a potenciálnej energie v bode l
konzervatívneho silového poľa je rovnaký ako súčet v bode 2. Keďže body
1 a 2 môžu byť ľubovoľné, súčet kinetickej a potenciálnej energie hmotného
bodu, ktorý budeme nazývať mechanickou energiou E hmotného
bodu, je v každom mieste konzervatívneho silového poľa rovnaký. Na základe
uvedeného môžeme rovnicu (2.3.30) zapísať vo všeobecnejšom
tvare
E = Ek + Ep =
konšt.
(2.3.31)
Táto rovnica je matematickým vyjadrením zákona zachovania mechanickej
energie, podľa ktorého súčet kinetickej a potenciálnej energie (mechanická energia)
hmotného bodu je rovnaký v každom mieste
konzervatívneho silového poľa (obr. 2.3.12).
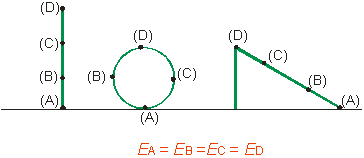
Obr. 2.3. 12: Mechanická energia je v každom bode konzervatívneho silového poľa rovnaká.
| a | Pomocou apletu (úloha 7) overte platnosť zákona zachovania mechanickej energie pri šikmom vrhu. |
V prírode a v technickej praxi sa stretávame s nekonzervatívnymi silami, ktoré
sa nazývajú disipatívne sily. Práca vykonaná nekonzervatívnymi
silami závisí od tvaru trajektórie ( od veľkosti dráhy medzi uvažovanými
bodmi), po ktorej sa pôsobisko sily pohybuje. Je zrejme, že práca nekonzervatívnych
síl po uzavretej trajektórií je na rozdiel od práce konzervatívnych síl rôzna
od nuly. Príkladom takej sily je sila trenia a aj
pohyb telesa v poli zemskej
tiaže, pri ktorom je potrebné zohľadniť odpor vzduchu je pohyb v
disipatívnom silovom poli.
Zákon zachovania mechanickej energie je špeciálnym prípadom zákona
zachovania energie, ktorý sa vzťahuje na všetky druhy energie.V prípade
disipatívnych síl akými sú napr. trecie sily, časť mechanickej energie sa
mení na tepelnú energiu, avšak celková energia sa zachováva.
| a | Pomocou apletu (úloha 1) pozorujte, ktoré zložky energie prispievajú k celkovej energii pri pohybe závažia na pružine. |