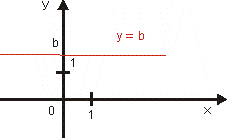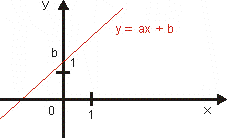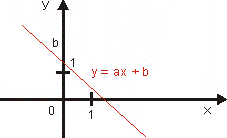funkcie

Matematicko - fyzikálne tabuľky

Funkcie1. 4/7

Lineárna funkcia
Kvadratická funkcia
Nepriama úmernosť
Logaritmická funkcia
Exponenciálna funkcia
Mocninová funkcia
Goniometrická funkcia

Lineárna funkcia
Lineárna funkcia sa nazýva každá funkcia na množine R daná rovnicou y = ax + b,

Vlastnosti lineárnej funkcie v závislosti od hodnôt parametra a sú zapísané v tabuľke Tab. 1.
Grafom lineárnej funkcie v karteziánskej súradnicovej sústave je vždy priamka rôznobežná s osou y.

Funkcia y = ax + b

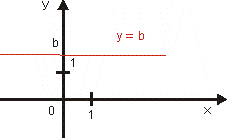
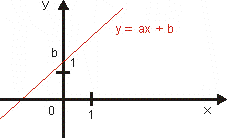
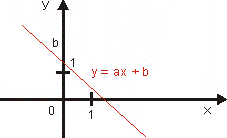
a = 0
Obor hodnôt je
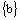
Nie je prostá (teda ani rastúca ani klesajúca)
Je ohraničená.

V každom bode má maximum i minimum.

a > 0
Obor hodnôt je R.
Je rastúca.
Nie je ani zhora ani zdola ohraničená.

Nemá ani maximum ani minimum.

a < 0
Obor hodnôt je R.
Je klesajúca.
Nie je ani zhora ani zdola ohraničená.

Nemá ani maximum ani minimum

Tab. 1: Vlastnosti lineárnej funkcie.

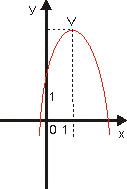
Kvadratická funkcia
Kvadratická funkcia sa nazýva každá funkcia na množine R daná rovnicou y = ax² + bx +c, .

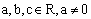Vlastnosti kvadratickej funkcie v závislosti od hodnôt parametra a sú zapísané v tabuľke Tab. 2.
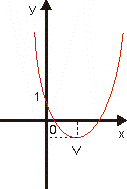
Grafom kvadratickej funkcie je parabola.

Funkcia y = ax² + bx +c,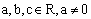


a > 0 Obor hodnôt je Klesajúca na Je rastúca na Je zdola ohraničená, nie je zhora ohraničená. V bode má ostré minimum.	a < 0 Obor hodnôt je Je rastúca na Je klesajúca na Je zhora ohraničená, nie je zdola ohraničená. V bode má ostré maximum.

Tab. 2: Vlastnosti kvadratickej funkcie.

Os paraboly je rovnobežná s osou y a súradnice vrchola paraboly sú:

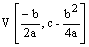
Parabola má priesečníky:
s osou y, x = 0, y = c, bod [0, c]
s osou x, y = 0, ax² + bx + c = 0
(ak je diskriminant tejto kvadratickej rovnice nezáporný, jej korene sú súradnice priesečníkov paraboly s osou x).

Nepriama úmernosť
Nepriama úmernosť sa nazýva funkcia definovaná na množine 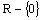daná rovnicou .
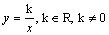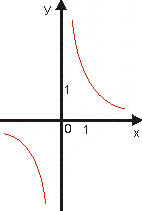
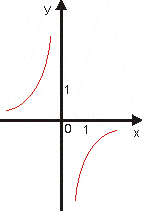
Grafom nepriamej úmernosti je hyperbola.
Vlastnosti nepriamej úmernosti v závislosti od parametra k sú v tab.3.

Funkcia

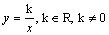
k > 0	k < 0
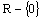
Obor hodnôt je	Obor hodnôt je
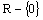
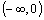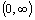
Je klesajúca na a na	Je rastúc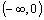a na a na

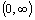
Nie je ani zhora ani zdola ohraničená.
Nemá ani maximum ani minimum.
je nepárna.

Tab. 3: Vlastnosti funkcie nepriama úmernosť.

Logaritmická funkcia
Logaritmickou funkciou so základom a sa nazýva funkcia inverzná k exponenciálnej funkcii y = a^x kde .
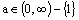Exponenciálna funkcia f: y = a^x obsahuje dvojice .
K nej inverzná je f ^-1: x = a^y zapisujeme ju: y = log_ax.
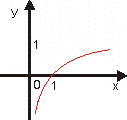
Grafom logaritmickej funkcie je logaritmická krivka. Vlastnosti logaritmickej funkcie udáva tabuľka Tab. 4.

Funkcia y = log_ax

a > 1	0 < a < 1

Definičný obor je
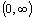
Obor hodnôt je R
Je rastúca a teda je prostá.	Je klesajúca, teda je prostá.
Nie je zhora ani zdola ohraničená Nemá ani minimum, ani maximum. Funkčná hodnota v bode 1 sa rovná 0.

Tab. 4: Vlastnosti logaritmickej funkcie.