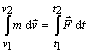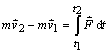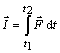Impulz sily

Z praxe vieme, že ak chceme dobre pribiť klinec do steny, musím po ňom buchnúť nejakou silou v krátkom časovom okamihu. V opačnom prípade, ak by úder po klinci trval veľmi dlho, mohol by klinec zo steny vypadnúť. Prečo je to tak, aká fyzikálna veličina to ovplyvní?

Doteraz sme hodnotili účinok sily z hľadiska dráhy, po ktorej pôsobila sila na hmotný bod, teda z hľadiska konania práce. V prípade pribíjania klinca do steny alebo pri golfe a tenise, nás zaujíma akú veľkú silu musíme vyvinúť za krátky časový interval tak, aby úder bol čo najúčinnejší. Teda nás zaujíma pôsobenie sily na hmotný bod za určitý časový interval.

Nech na hmotný bod pôsobí sila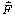, ktorú popíšeme pomocou pohybovej rovnice
 

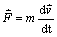
a upravíme na tvar .      (2.3.11)

Integrovaním tohto vzťahu od okamihu t₁ = 0, kedy sila začala pôsobiť na hmotný bod, ktorý mal v tomto okamihu rýchlos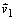ť , po okamih t₂, kedy končí silové pôsobenie a hmotný bod má rýchlosť

 
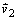
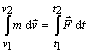
potom 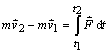      .        (2.3.12)


Výraz na pravej strane (2.3.12) vyjadruje impulz sily, ktorý je definovaný pomocou časového integrálu
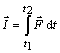                       (2.3.13)


V prípade, že pôsobiaca sila na teleso je konštantná impulz sily

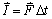.            (2.3.14)


Fyzikálna veličina impulz hodnotí časový účinok sily a pomocou nej môžeme hodnotiť nárazové sily. Jej jednotkou je 1 newtonsekunda (I) = N.s, (1 Ns = kg.m/s). Je to impulz konštantnej sily s absolútnou hodnotu 1 N, ktorej účinok trval 1 s.

Zo vzťahu (2.3.13) vyplýva, že smer impulzu je daný smerom pôsobiacej sily a jeho veľkosť závisí od veľkosti sily.

Kontrolka: Ktorý vzťah použijete pri výpočte impulzu sily, ak na teleso pôsobí sila, ktorá je daná:
a) F = 3t + 4 (N)
b) F = 5 N.