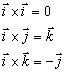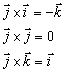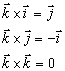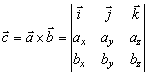Rozklad vektora na zložky
Vo fyzike často potrebujeme nahradiť jeden vektor dvoma alebo viacerými vektormi, ktorých súčet predstavuje pôvodný vektor. Existuje však mnoho možností rozkladu príslušného vektora na zložky.  Rozklad sa stane jednoznačným, keď predpíšeme nejaké vedľajšie podmienky. Často požadujeme, aby zložky rozkladového vektora boli navzájom kolmé. Pre tento účel je výhodné rozkladať vektor na zložky ležiace v osiach pravouhlej súradnicovej sústavy. Uvažujme o pravouhlej súradnicovej sústave s osami X, Y, Z a s jednotkovými vektormi 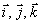v smere príslušných osí. Nech vektor 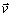má začiatok v začiatočnom bode O uvažovaného súradnicového systému (Obr. 8). Keď zložky vektora 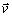 v smere súradnicových osí označíme 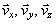 potom môžeme písať

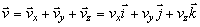
kde v_x, v_y a v_z  sú veľkosti jednotlivých zložiek (súradnice vektora ).

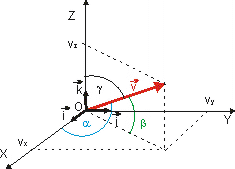
Obr. 8: Rozklad vektora na zložky.

Pre veľkosť vektora platí .


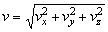Smer vektora 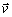môžeme vyjadriť pomocou uhlov a, b, g, ktoré zviera vektor 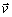s jednotkovými vektormi . 
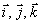Z obr. 8 pre jednotlivé uhly vyplývajú vzťahy (smerové kosíny)



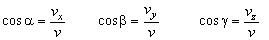
Nech a_x, a_y, a_z, b_x, b_y, b_z  sú súradnice vektorov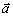a 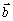v pravouhlom súradnicovom systéme, takže platí
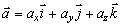a .


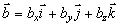Pre súčet resp. rozdiel vektorov 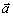a môžeme písať 

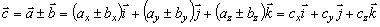
kde  , , .



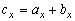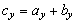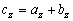Podľa definície skalárneho súčinu pre jednotlivé vektory 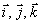platia vzťahy
             



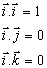
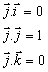
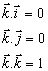
Ak skalárny súčin dvoch vektorov 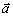a 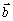 vyjadríme pomocou ich zložiek, dostaneme

 


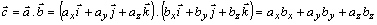
Pre vektorový súčin medzi jednotlivými vektormi 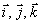   je možné písať vzťahy 
     



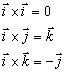
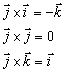
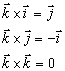
Vektorový súčin vektorov 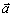 a 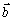vyjadrených pomocou zložiek je vektor 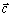,  pre ktorý platí




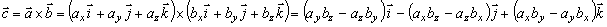
čo je možné vyjadriť aj pomocou determinantu 

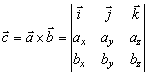
Diferenciálne a integrálne operácie s vektormi
Nech vektora 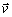, ktorý môže byť vyjadrený pomocou zložiek v pravouhlej súradnicovej sústave, je vektorovou funkciou skalárnej premennej t.j. .

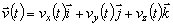Derivácia tohto vektora podľa skalárnej premennej t je vektor 


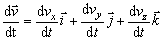
ktorého zložky sú rovné deriváciám zložiek vektora .

Integrál vektora je vektor 


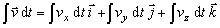
ktorého zložky sa rovnajú integrálom zložiek vektora .

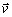Nech vektory 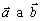sú vektorovými funkciami skalárnej premennej, t.j. 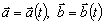. Pre deriváciu skalárneho resp. vektorového súčinu vektorov 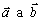platia vzťahy

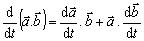
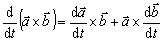
Ďalšie zdroje:
http://www.kf.elf.stuba.sk/~cerven  v časti domáce animácie si pozrite Rýchlokurz vektorov