Pomocou vzťahu pre elementárnu zmenu potenciálnej energie
(2.3.26)
vyplývajúceho z rovnice (2.3.24) môžeme odvodiť závislosť sily od potenciálnej energie v danom mieste silového poľa. Potenciálna energia hmotného bodu Ep závisí od jeho polohy v konzervatívnom silovom polí, ktorá môže byť určená pomocou súradníc x, y a z. Pre diferenciál dEp funkcie Ep (x, y, z) platí
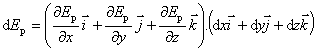(2.3.27)
Výraz na pravej strane poslednej rovnice, ktorý označíme pomocou symbolu
(nabla) t.j. 
,predstavuj diferenciálny operátor a výsledkom jeho pôsobenia na skalárnu veličinu je vektor. Operáciu operátora
,
ktorý sa nazýva aj Hamiltonov operátor, na skalárnu veličinu
nazývame gradient. Pomocou tohto označenia môžeme rovnicu
(2.3.27) vyjadriť v tvare
. (2.3.28)
Vektor
vyjadruje elementárne posunutie hmotného bodu. Porovnaním vzťahov (2.3.26) a (2.3.28) dostávame rovnicu
,ktorá hovorí, že sila, ktorou konzervatívne silové pole pôsobí v danom mieste na hmotný bod, je rovná záporne vzatému gradientu jeho potenciálnej energie v uvažovanom mieste.