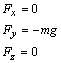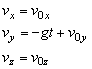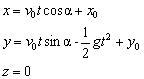Pohybové
rovnice majú široké uplatnenie v rôznych oblastiach fyziky a technickej
praxe. Použitím týchto rovníc popíšeme pohyb telesa v poli
zemskej tiaže.
Pohyb
telesa v poli zemskej tiaže
Tiažová sila, ktorou pôsobí Zem na padajúce telesá závisí
od ich polohy
v okolí Zeme. Pri popise pohybu telesa resp. hmotného bodu v poli zemskej tiaže budeme
predpokladať, že sa uskutočňuje v dostatočne malom priestore, v ktorom
v každom bode tiažová sila pôsobiaca na teleso môže byť považovaná za konštantnú (z hľadiska
smeru aj veľkosti - homogénne tiažové pole). Nech hmotnému bodu
hmotnosti m je udelená rýchlosť
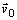 , ktorá zviera s vodorovným
smerom uhol α. Pre lepší
popis položme rovinu OXY do zvislej
roviny, v ktorej leží smer rýchlosti (tak, že os OX je vodorovná, os
OY je zvislá a os
OZ je kolmá k obom predchádzajúcim osiam)
(Obr. 2.2.1). Počiatok súradnicového
systému umiestnime do miesta, v ktorom hmotnému bodu je udelená rýchlosť
, ktorá zviera s vodorovným
smerom uhol α. Pre lepší
popis položme rovinu OXY do zvislej
roviny, v ktorej leží smer rýchlosti (tak, že os OX je vodorovná, os
OY je zvislá a os
OZ je kolmá k obom predchádzajúcim osiam)
(Obr. 2.2.1). Počiatok súradnicového
systému umiestnime do miesta, v ktorom hmotnému bodu je udelená rýchlosť
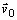 .
.
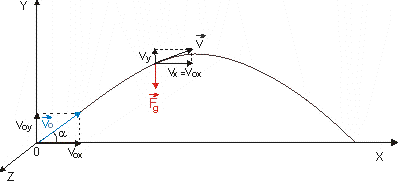
Obr. 2.2.1: Pohyb hmotného bodu v poli zemskej tiaže.
| a |
Pozrite si aplet
(úloha 1), ktorý
simuluje tento pohyb. |
Na hmotný
bod v ľubovoľnom mieste dráhy pôsobí tiažová sila
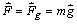 , ktorej súradnice v uvažovanom systéme sú
, ktorej súradnice v uvažovanom systéme sú
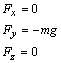 (2.2.5)
(2.2.5)
Súčasne môžme tento
pohyb popísať pomocou pohybových rovníc
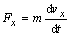
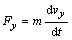
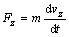 . (2.2.6)
. (2.2.6)
Kontrolka:
Koľko
síl pôsobí na hmotný bod počas pohybu v poli zemskej tiaže? Aký je ich
smer počas pohybu, mení sa?
Odvodenie
súradníc rýchlosti
Tiažová sila pôsobiaca na teleso pri vrhu je konštantná
(je to druhý typ pohybovej rovnice), preto na odvodenie súradníc rýchlosti
použijeme už odvodené vzťahy (2.2.3)
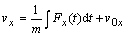
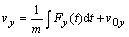
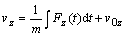
Dosadením
súradníc
tiažovej sily (2.2.5) do týchto rovníc
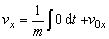 (2.2.7a)
(2.2.7a)
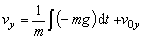 (2.2.7b)
(2.2.7b)
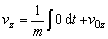 (2.2.7c)
(2.2.7c)
a ich úpravou
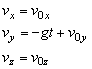 .
(2.2.8)
.
(2.2.8)
Z obr.2.2.1 pre súradnice počiatočnej rýchlosti (v čase t
= 0 s) pohybu
platí
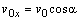
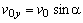
ktorých dosadením do
(2.2.8) pre súradnice rýchlosti
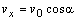 (2.2.9a)
(2.2.9a)
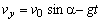 (2.2.9b)
(2.2.9b)
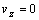 (2.2.9c)
(2.2.9c)
| a |
Pomocou apletu
(úloha 2) pozorujte smer a veľkosť jednotlivých zložiek rýchlosti (x - ovú
a y - ovú) počas pohybu. Menia sa? |
Kontrolka:
V ktorom bode trajektórie bude smer aj veľkosť rýchlosti hmotného bodu rovná len x - ovej
súradnici rýchlosti? Svoju odpoveď odôvodnite.
Odvodenie
súradníc dráhy pohybu
Súradnice dráhy
pohybu vypočítame pomocou rovníc (2.2.4), kde za
súradnice rýchlosti dosadíme rovnice (2.2.9). Integrovaním
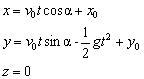 ,
,
kde z počiatočných podmienok
(v t = 0 s pre hmotný bod
x = y = z = 0)
potom x0 = y0
= z0 = 0.
Súradnice dráhy môžeme popísať rovnicami
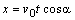 (2.2.10a)
(2.2.10a)
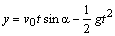 (2.2.10b)
(2.2.10b)
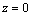 (2.2.10c)
(2.2.10c)
 |
Z rovnice
(2.2.10c) vyplýva, že celá dráha hmotného
bodu počas pohybu leží v rovine
OXY, lebo súradnica
z je stále nulová. |
Rovnice (2.2.9) a (2.2.10) popisujú
pohyb telesa v poli zemskej tiaže. V závislosti od uhla α rozlišujeme
následovné špeciálne prípady:
1. α = 00
dostávame rovnice pre vodorovný vrh,
2.
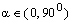 šikmý
vrh,
šikmý
vrh,
3.
α = 900
zvislý vrh nahor,
α = - 900 zvislý vrh nadol,
α = - 900
a
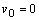 voľný
pád.
voľný
pád.
| a |
Pomocou apletu
(úloha 3) pozorujte tvar trajektórie, hodnoty
a smery zložiek rýchlosti ako aj uhol medzi počiatočnou rýchlosťou a
vodorovným smerom. |
Kontrolka:
Ako sa líši trajektória pohybu hmotného bodu pri šikmom vrhu a zvislom
vrhu nadol? Ako sa líši šikmý vrh od vodorovného z hľadiska smeru počiatočnej
rýchlosti?
Príklad 2.2.5
 |
Ak je teleso vrhnuté z konkrétnej výšky nad povrchom
Zeme, teda nie z povrchu Zeme (z počiatku súradnicového
systému), súradnice
dráhy telesa sú dané rovnicami 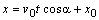
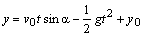 (2.2.11). Súradnice x0,
y0
predstavujú
súradnice polohy hmotného bodu, z ktorého je teleso vrhnuté v danej výške
(počiatočný bod). (2.2.11). Súradnice x0,
y0
predstavujú
súradnice polohy hmotného bodu, z ktorého je teleso vrhnuté v danej výške
(počiatočný bod).
|
Príklad
2.2.6
| a |
V aplete
(úloha 4) pri daných počiatočných podmienkach pozorujte pohyb hmotného
bodu. |
Trajektória
pohybu pri šikmom vrhu je parabola.
Odvodené rovnice (2.2.9) a (2.2.10) platia pre pohyb hmotného bodu vo vákuu. Vplyv odporu
prostredia ako aj rotácie
Zeme sme zanedbali.
Pozri ešte: Aplikácie
pohybovej rovnice