Príklad 2.2.1: Výpočet sily pôsobiacej na hmotný bod pohybujúci sa po kružnici. Vypočítajte silu pôsobiacu na hmotný bod o hmotnosti m, ktorý sa pohybuje po kružnici polomeru r, ak jeho poloha v pravouhlej súradnicovej sústave je určená polohovým vektorom , kde r a sú konštanty.

Riešenie: Keďže je daná (známa) poloha hmotného bodu, na výpočet sily použijeme rovnicu    (1)
z ktorej vyplýva, že musíme dvakrát zderivovať polohový vektor podľa času:  

.      (2)
                                                                                            

Dosadením vzťahu (2) do rovnice (1) pre silu (3), kde výrazy pred jednotkovými vektormi predstavujú súradnice zložiek sily F_x a F_y .    
Pre veľkosť sily potom       (4)
a dosadením za súradnice , do vzťahu (4), sila .
Ďalšími matematickými úpravami , pričom veličiny m, r, sú konštanty. Teda veľkosť sily je konštantná.

Keďže sila je vektorová veličina, bude nás zaujímať aj jej smer. Použijeme rovnicu (3), ktorú upravíme do tvaru, kde výraz v zátvorke predstavuje polohový vektor . Teda pre smer sily . Z tohto zápisu je zrejme, že sila má opačný smer ako polohový vektor . 

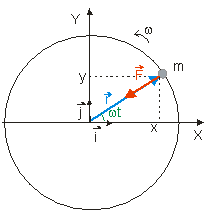
Obr. 2.2.1: Na hmotný bod pôsobí sila, ktorá je konštantná a smeruje vždy do počiatku súradnicového systému.

Z odvodených vzťahov vyplýva, že sila má konštantnú veľkosť a jej smer sa nemení , smeruje v každom okamihu do počiatku súradnicovej  sústavy (Obr. 2.2.1). Je to dostredivá sila, ktorá spôsobuje rovnomerný otáčavý pohyb po kružnici s konštantnou uhlovou rýchlosťou . Veľkosť a smer tejto sily možno určiť aj pomocou rovníc (2.4.4), (2.4.6).

Späť

Príklad 2.2.2: Teleso hmotnosti 5 kg sa pohybuje účinkom časovo premennej sily , kde A = 25 N, B = 10 N/s. Za koľko sekúnd sa teleso zastaví, ak v čase 0 s malo rýchlosť 6 m/s a sila mala opačný smer rýchlosti? Akú dráhu prejde teleso do zastavenia?

Riešenie: Zo zadania úlohy vyplýva, že sila, ktorá pôsobí na teleso je známa, teda ide o druhý typ úloh. Navyše sa sila mení s časom. Na výpočet časového intervalu, za ktorý sa teleso zastaví, použijeme vzťah pre súradnicu rýchlosti (2.2.3a), ktorý vyplýva z pohybovej rovnice 
 odtiaľ    
(v ďalšom popise index x nebudeme používať). Potom dosadením za silu pre rýchlosť 


po integrácií a úprave, pre rýchlosť dostávame

.             (1)

  Zaujíma nás doba, za ktorú sa teleso zastaví, preto zavedieme podmienku, že v čase zastavenia t_z je koncová rýchlosť v = 0 m/s. Potom
,
 
odtiaľ po dosadení čísel úpravou dostaneme kvadratickú rovnicu . Jej riešením t_z = 6 s, teleso sa zastaví za 6 s.


Pri výpočte dráhy, ktorú prejde teleso do zastavenia použijeme rovnicu (2.2.4a)
   resp.         (2)

Dosadením rýchlosti (vzťah (1)) do (2) 


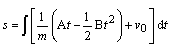
kde s₀ = 0 m.  Po integrovaní a úprave dráha do zastavenie je 
,


kde za čas dosadíme t_z = 6 s. Riešením vychádza, že dráha do zastavenia je s_z = 54 m.

Späť

Príklad 2.2.3: Pri rozbiehaní motorového vozidla z pokoja pôsobí na neho sila v smere rýchlosti, ktorá je nepriamoúmerná rýchlosti t.j.  kde k je konštanta. Odvoďte  závislosť rýchlosti a dráhy vozidla od času.

Riešenie: Opäť zo zadania príkladu vyplýva, že ide o druhý typ pohybovej rovnice (sila je známa). Na odvodenie časovej závislosti rýchlosti vozidla použijeme rovnicu (2.2.2a)
    (1)

(súradnicu x v ďalšom popise nebudeme používať). V tomto prípade sila nezávisí od času, ale od rýchlosti, preto pri odvodzovaní rýchlosti budeme upravovať diferenciálnu rovnicu, ktorú dostaneme tak, že do vzťahu (1) dosadíme za silu konkrétny predpis ,
.

Separáciou premenných (na jednej strane rovnice necháme všetky veličiny, ktoré sa týkajú rýchlosti, teda toho čo chceme vypočítať a všetky ostatné prenesieme na druhú stranu tak, aby dv a dt neboli ani na jednej strane v menovateli) upravíme rovnicu do tvaru
.

Pravú aj ľavú stranu rovnice budeme integrovať v hraniciach pre čas od 0 po t a rýchlosť od v₀ po v 
 

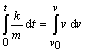
odtiaľ

.

 Zo zadania vyplýva, že vozidlo sa rozbieha z pokoja (v₀ = 0 m/s), potom pre časovú závislosť rýchlosti vozidla
   (2)


Na odvodenie závislosti dráhy prejdenej vozidlom od času použijeme rovnicu (2.2.4a) resp.


kde za rýchlosť dosadíme odvodený vzťah (2), pričom s₀ = 0 m (rozbieha z pokoja). Integrovaním v hraniciach od 0 po t pre časovú závislosť dráhy vozidla dostávame
   (3)


Odvodené časové závislosti rýchlosti vozidla a prejdenej dráhy sú dané vzťahmi (2) a (3).

Ak by sme chceli v tomto príklade vypočítať dobu, za ktorú teleso zväčšilo svoju rýchlosť na určitú hodnotu, separácia premenných by mala iný tvar. Na jednej strane by sme nechali čas a na druhú stranu by sme preniesli všetky ostatné veličiny , tento tvar by sme potom integrovali.

Späť

Príklad 2.2.4: Teleso sa dáva do pohybu pôsobením sily F = 0,02 N a za prvé 4 s svojho pohybu prejde dráhu 3,2 m. Aká veľká je jeho hmotnosť a akú rýchlosť má na konci svojho pohybu, ak sila pôsobí na teleso v smere dráhy?

Riešenie: Aby sme mohli vypočítať hmotnosť telesa musíme najprv odvodiť rovnicu pre rýchlosť a dráhu telesa pri rozbiehaní. Na teleso pôsobí sila v smere pohybu (napr. v smere x), preto použijeme na odvodenie rýchlosti rovnicu (2.2.3a)


kde v ďalšom popise nebudeme používať index x. Sila je konštantná, môžeme ju vybrať pred integrál 
 
po  integrovaní   (1).  

Zo zadania vyplýva, že počiatočná rýchlosť bola nulová, preto v₀ = 0 m/s. Na odvodenie dráhy použijeme rovnicu  (2.2.4a), resp.

 , kde za rýchlosť dosadíme vzťah (1)
. 

Po integrovaní pre dráhu 

,    (2)

kde s₀ = 0 m. Na výpočet hmotnosti telesa použijeme vzťah (2), v ktorom dráha, sila a čas sú známe  veličiny. Úpravou


,    (3)
   .

Rýchlosť telesa v čase 4 sekundy vypočítame pomocou vzťahu (1), do ktorého dosadíme za hmotnosť vzťah (3). Úpravou pre rýchlosť
.

Hmotnosť telesa je 0,05 kg a jeho rýchlosť v štvrtej sekunde je 1,6 m.

Tento príklad by sme môžeme riešiť aj iným spôsobom. Ak si uvedomíme, že pôsobiaca sila je konštantná a navyše pôsobí na hmotný bod v smere dráhy, znamená to, že teleso vykonáva priamočiary pohyb s konštantným zrýchlením (F - konš. potom a - konšt.). Ide teda o rovnomerne zrýchlený priamočiary pohyb, ktorého rýchlosť a dráhu vieme popísať rovnicami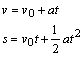   .   Použitím týchto rovníc a vzťahu pre silu F = ma sa dajú odvodiť tie isté vzťahy ako pri prvom spôsobe riešenia. Vyskúšajte si to.

Späť

Príklad 2.2.5: Delová guľa opúšťa hlaveň dela rýchlosťou v₀ = 1000 m/s pod výškovým uhlom  55⁰. Treba vypočítať teoretickú dĺžku dostrelu a teoretickú maximálnu výšku, ktorú by guľa dosiahla, keby neexistoval odpor vzduchu.

Riešenie: Zo zadania príkladu vyplýva, že delová guľa, ktorá je vrhnutá z povrchu Zeme, vykonáva šikmý vrh . Pri výpočte budeme vychádzať z rovníc, ktoré popisujú šikmý vrh
            (1a)
      (1b)
            (1c)
  (1d)

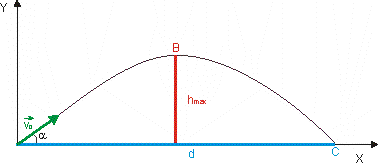
Obr. 2.2.2

Z obrázku obr. 2.2.2 vyplýva, že teoretickú maximálnu výšku predstavuje bod B a teoretickú maximálnu dĺžku bod C. 
V bode C popíšeme súradnice polohy gule nasledovne x = d, y = 0  (2). Dosadením podmienok (2) do rovníc (1c) a (1d)
(3a)
. (3b)


Z rovnice (3b) pre dobu


a dosadením do  rovnice (3a) pre maximálny dostrel



Teoretická dĺžka dostrelu gule by bola 95,7 km.


Pri výpočte maximálnej výšky pre guľu v bode B platia nasledovné podmienky:
  (4)

(v bode B celková rýchlosť má smer x - ovej súradnice, pričom y - ová súradnica rýchlosti je nulová).
Dosadením podmienok (4) do rovníc (1b) a (1d) dostávame
(5a)
.            (5b)

Úpravou rovnice (5b) dostávame dobu, ktorý dosadíme do rovnice (5a).  Pre maximálnu výšku



Maximálna výška, ktorú guľa teoreticky dosiahne je 34,1 km.

 Späť

Príklad 2.2.6: Pri filmovej naháňačke má kaskadér preskočiť na strechu susednej budovy. Ešte predtým ho prezieravo napadne, či vôbec môže túto úlohu zvládnuť, ak beží po streche susednej budovy nanajvýš rýchlosťou 4,5 m/s. Strecha susednej budovy je  o 4,8 m nižšie ako strecha budovy, po ktorej beží kaskadér a jej vzdialenosť od susednej budovy je 6,2 m. Má kaskadér skočiť alebo radšej nie?

Riešenie: Pri riešení tohto problému nás zaujíma ako ďaleko doletí kaskadér vo vodorovnom smere za dobu t. Zvoľme si súradnicový systém tak ako je to znázornené na obr.2.2.3. Zo zadania príkladu vyplýva, že pohyb kaskadéra predstavuje vodorovný vrh, pretože smer jeho rýchlosti na začiatku skoku je totožný s vodorovným smerom. Rovnice pre vodorovný vrh dostaneme z rovníc (2.2.11), kde uhol α = 0⁰. Pohyb kaskadéra popisujú rovnice:  
(1)
. (2)

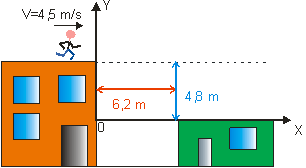
Obr. 2.2.3

Vychádzajúc  z obr. 2.2.3, platia nasledujúce podmienky: x₀ = 0 m, y₀ = 4,8 m a pre bod, do ktorého doskočí x = d,  y = 0 m  (3). Využitím týchto podmienok a úpravou rovnice (2) potom pre časový interval, za ktorý kaskadér skočí na susednú strechu
 .


Dosadením do rovnice (1), pri využití podmienok (3) a x₀ = 0 mvypočítame vzdialenosť, do ktorej kaskadér doskočí
m.     

Vzdialenosť, do ktorej kaskadér doskočí je 4,5 m. Keďže vzdialenosť susednej budovy je 6,2 m,  kaskadér nemá skákať.

Späť