1.
|
V nasledujúcich zadaniach úloh, vyberte o ktorý
typ pohybovej rovnice ide:
a) Loptička hmotnosti 50 g sa pohybuje po krivke, ktorej súradnice sú
dané: x = 3t2, y = 2t, z = 3.
Vypočítajte veľkosť sily pôsobiacej na loptičku v čase 3 s.
b) Teleso hmotnosti 1 kg sa pohybuje po priamke rýchlosťou v0
= 3 m/s. V určitom okamihu začne na teleso pôsobiť urýchľujúca
sila, ktorá je priamoúmerná času. Vypočítajte, akú bude mať rýchlosť
a akú dráhu prejde za 2 sekundy, ak k = 6 N/s.
c) Guľôčka s hmotnosťou m
a počiatočnou rýchlosťou v0 sa
pohybuje tak, že odpor prostredia rastie lineárne s rýchlosťou
guľôčky. Akú dráhu prejde do zastavenia, ak na ňu nepôsobí
žiadna iná sila?
d) Aká je veľkosť sily, pôsobiacej na časticu hmotnosti m = 5
g v čase t = 1 s, ak rýchlosť častice závisí od času:
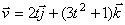 . .
(a, d - prvý typ, b, c - druhý typ)
|
2.
|
Vyriešte úlohy z predchádzajúceho zadania.
Ktoré vzťahy pri výpočte použijete?
( a) F = 0,3 N, b) v = 15 m/s, s = 14 m, c) s
= (mv0)/k,
d)
F = 0,031 N)
|
3.
|
V Galileiovom diele Rozpravy o 2 nových vedách
sa dočítame: ,, ... pre dva rôzne elevačné uhly, ktoré sa líšia
od uhla 450 o rovnakú hodnotu, je dĺžka letu rovnaká...
." Dokážte pravdivosť tohto tvrdenia (overte si
platnosť tohto výroku pomocou apletu
- úloha 6).
|
4.
|
Z dela
pobrežného delostrelectva umiestneného vo výške
h = 30 m
nad hladinou mora je vypálená strela pod uhlom 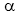 = 45o
vzhľadom na horizontálnu rovinu s počiatočnou rýchlosťou v0
= 1000 ms-1. Aká je vodorovná
vzdialenosť miesta, v ktorom
strela zasiahne cieľ ležiaci na hladine mora, od dela? (x = 102
km) = 45o
vzhľadom na horizontálnu rovinu s počiatočnou rýchlosťou v0
= 1000 ms-1. Aká je vodorovná
vzdialenosť miesta, v ktorom
strela zasiahne cieľ ležiaci na hladine mora, od dela? (x = 102
km)
|
5.
|
Z určitej výšky h sme vyhodili súčasne
dve telesá, jedno nahor a druhé nadol s počiatočnou rýchlosťou v0.
Určte závislosť ich vzájomnej vzdialenosti od času. (d = 2v0t)
|
6.
|
Teleso voľne padajúce má v určitom mieste A rýchlosť
50 cm/s. Nájdite dobu, za ktorú teleso prejde vzdialenosť AB, keď v
mieste B má rýchlosť 250 cm/s. Aká veľká je vzdialenosť AB?
(t = 0,204 s, d = 0,3 m) |

