Pohyb nabitej častice v homogénnom
elektrickom poli
Podobne ako pri šikmom vrhu sme uvažovali o poli zemskej tiaže, že je homogénne,
rovnako aj v tomto prípade budeme predpokladať, že elektrické pole je homogénne.
Elektrické pole charakterizuje vektorová veličina intenzita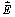
, ktorej veľkosť aj smer sa v každom bode homogénneho elektrického poľa
nemení,
je konštantná (viac sa dozviete o elektrickom poli v 2. ročníku). Zvoľme smer elektrického
poľa resp. intenzity zvislo
nadol (obr. 2.6.4). Nech do tohto poľa vletí kolmo na smer intenzity kladne nabitá
častica s počiatočnou rýchlosťou
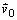, ktorej hmotnosť je m a náboj q.
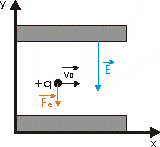
Obr. 2.6.4: Kladné nabitá častica
vletí kolmo do homogénneho elektrického poľa.
V elektrickom poli na ňu pôsobí
sila, ktorá je daná vzťahom
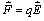v smere elektrického poľa (intenzity ),
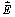potom súradnice sily
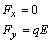(2.6.4)
Chceme vedieť, aký pohyb bude nabitá častica v tomto poli vykonávať, t.j.
zaujíma nás jej rýchlosť a dráha, ktorú prejde za dobu t. Ide o
druhý typ pohybovej rovnice (sila je daná, v, s - treba vypočítať),
navyše sila je konštantná. Pri výpočte rýchlosti použijeme vzťahy (2.2.3), kde za silu dosadíme vzťahy
(2.6.4)
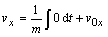
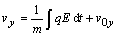
integrovaním
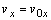(2.6.5)
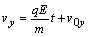. (2.6.6)
Z počiatočných podmienok vyplýva, že
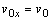a
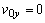, potom
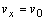(2.6.7)
.
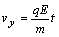(2.6.8)
Na odvodenie dráhy častice použijeme rovnice (2.2.4), kde za súradnice rýchlosti
dosadíme vzťahy (2.6.7) a (2.6.8)
.
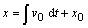
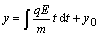Integrovaním
.
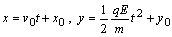Použitím počiatočných podmienok
x0
= y0 = 0, súradnice dráhy
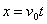(2.6.9)
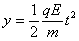(2.6.10)
Z rovníc (2.6.7) a (2.6.9) vyplýva, že častica vykonáva v smer osi x
rovnomerný priamočiary pohyb a v smere osi y ide o rovnomerne zrýchlený
priamočiary pohyb, čo vyplýva s rovníc (2.6.8) a (2.6.10), kde
.
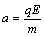Nabitá častica je počas pohybu v elektrostatickom poli vychyľovaná
vplyvom elektrostatickej sily a navyše dochádza k zakriveniu jej dráhy resp. k vychýleniu
z pôvodného smeru pohybu nadol. V prípade častice so záporným znamienkom,
by pri tých istých podmienkach došlo k vychýleniu častice smerom nahor.
Odvodené rovnice (2.6.7) - (2.6.10) platia pre špeciálny prípad. Riešenie podobných
úloh závisí od počiatočných podmienok a zadania úlohy.
|
|
Pôsobenie
elektrického poľa na nabitú časticu sa uplatňuje pri
atramentovej tlačiarni, kde sa toto pôsobenie používa pri
nastrekovaní atramentu na papier. Kvapka atramentu sa nabije na zápornú
hodnotu v nabíjacej jednotke (obr. 2.6.5). Kvapka ďalej prechádza vychyľovacimi
doskami tlačiarne, medzi ktorými je homogénne
elektrické pole o intenzite E, ktorá smeruje nadol. Ako bolo vyššie
spomenuté, na záporne nabitú kvapku atramentu pôsobí pole
elektrostatickou silou, ktorá spôsobí jej vychýlenie smerom nahor. |
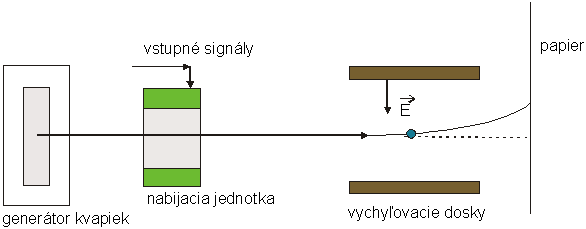
Obr. 2.6.5: Základný princíp
atramentovej tlačiarne.
Kvapka
potom dopadne na papier miesto,
ktoré závisí od veľkosti intenzity elektrického poľa E a náboja kvapky q.
V praxi sa postupuje tak, že sa necháva intenzita poľa konštantná a polohu
kvapky na papieri ovládame nábojom q,
ktorý získa kvapka v nabíjacej jednotke, kým vletí
do vychyľovacieho systému. Nabíjacia jednotka je riadená elektronickými signálmi z počítača,
ktorými určujeme náboj pridávaný každej kvapke,a tým jej polohu na papieri kde dopadne.
 |
Na
vytvorenie 1 znaku je potrebných asi 100 drobných kvapiek.
|