Pohyb nabitej častice po kružnici

Ak sa pohybuje častica rovnomerne po kružnici, potom výsledná sila, ktorá na ňu pôsobí musí mať konštantnú veľkosť a musí byť orientovaná do stredu kružnice. V príklade 2.2.1 sme vypočítali a ukázali, že je to dostredivá sila. Pôsobenie dostredivej sily sa uplatňuje aj v prípade pohybu nabitej častice, ktorá vletí kolmo do homogénneho magnetického poľa. 

Magnetické pole charakterizuje podobne ako elektrické vektorová veličina magnetická indukcia , pre ktorú v homogénnom magnetickom poli platí, že má rovnaký smer aj veľkosť v každom bode poľa (viac sa dozviete na Fyzike 2. v druhom ročníku).  

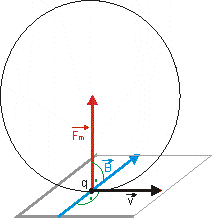
Obr. 2.6.6: Pohyb nabitej častice v homogénnom magnetickom poli.

Ak do tohto poľa vletí nabitá častica rýchlosťou kolmo na smer indukcie (obr. 2.6.6), začne na ňu pôsobiť magnetická sila , ktorá spôsobí, že častica sa bude pohybovať po kružnici.

Z definície smeru výsledného vektora vektorového súčinu vyplýva, že sila bude kolmá na rovinu vektorov a a bude smerovať nahor.

Vypočítame parametre (polomer r, periódu T, frekvenciu f, uhlovú rýchlosť w), ktoré charakterizujú tento pohyb častice s nábojom q s konštantnou rýchlosťou . Vplyvom magnetickej sily sa častica pohybuje po kružnici, jej veľkosť (vyplýva z vektorového súčinu) je daná F_m = qvB (2.6.11), pretože a , .

V úvode sme povedali, že ak sa pohybuje častica rovnomerne po kružnici, je to spôsobené dostredivou silou, ktorej veľkosť je F_d = mrw² (2.6.12) (pozri odvodenie v príklade 2.2.1) a v tomto prípade je daná silou F_m . Porovnaním (2.6.11) a (2.6.12)

F_m = F_d
qvB = mrw²


kde v = wr, potom úpravou pre polomer kružnice, po ktorej sa nabitá častica pohybuje



Pre periódu
        (2.6.13)

frekvenciu
                         (2.6.14)

a uhlovú rýchlosť
                          (2.6.15).

Zo vzťahov (2.6.13) - (2.6.15) vyplýva, že T,  f, w nezávisia od veľkosti rýchlosti častice.

Princíp pohybu nabitej častice v homogénnom poli sa uplatňuje aj pri magnetróne. Na obr. 2.6.6a je zobrazený magnetrón, ktorý sa používa na laboratórnych cvičeniach na našej katedre pri určovaní merného náboja elektrónu. Pozostáva z cievky a diódy, ktoré sú umiestnené tak, že ich osi sú rovnobežné (obr. 2.6.6b) a teda elektrické pole vytvorené diódou je kolmé na magnetické pole cievky. 

  Obr. 2.6.6: a) Magnetrón.  b) Dióda vo vnútri cievky.

Elektróny, ktoré sa uvoľňujú zo žeravenej katódy prechádzajú na anódu, pričom sú niektoré vychyľované vplyvom magnetického poľa cievky a pohybujú sa po kružnici. To sa využíva aj pri magnetróne v mikrovlnej rúre. Elektróny svojim krúživým pohybom generujú vlny, ktoré sú vysielané do rúry, kde zohrievajú potravu rozkmitaním molekúl vody.
Pôvodne bola magnetrónová technológia vyvinutá pre vojenské radarové systémy. V roku 1946 inžinier radarových systémov Percy Spencer si pri testovaní nového magnetrónu všimol, že kandizovaná tyčinka, ktorú mal vo vrecku sa roztopila. Potom to vyskúšal s pukancami, vajíčkom a inými potravinami, ktoré položil pred zariadenie. Všetko sa uvarilo a vajíčko dokonca vybuchlo. Odvtedy sa začala táto technológia využívať aj na varenia a ohrievanie potravy.