v ktorých za kladný smer je považovaný smer tiažovej sily, m je hmotnosť guľôčky, m´ je hmotnosť tekutiny s objemom rovným objemu guľôčky, k je konštanta.
| 2.6 Aplikácie pohybovej rovnice | Pohyb telesa vo viskóznej tekutine 1/4 |
Pohyb telesa vo viskóznej tekutine
V kapitole
pohybová rovnica sme pri skúmaní pohybu telesa v poli zemskej tiaže zanedbali
odpor
vzduchu. Často pri pohybe telesa v tekutine (v plyne alebo
kvapaline) nie je možne zanedbať odpor prostredia proti pohybu a ani vztlakovú
silu. V tejto časti ukážeme ako v tomto prípade postupovať pri popise
pohybu.
Pri pohybe telesa vo viskóznej
tekutine okrem tiaže treba zohľadniť ďalšie
dve sily. Odporová sila
![]() je namierená proti smeru pohybu a ak pohybujúcim telesom je guľôčka, potom
veľkosť tejto sily je úmerná rýchlosti guľôčky. Veľkosť vztlakovej
sily
je namierená proti smeru pohybu a ak pohybujúcim telesom je guľôčka, potom
veľkosť tejto sily je úmerná rýchlosti guľôčky. Veľkosť vztlakovej
sily
![]() sa určí podľa Archimedovho zákona. Táto sila je opačne orientovaná ako
tiažová sila, pôsobiaca na teleso pri pohybe v tekutine. Všetky tri sily ležia
v tej istej priamke (obr. 2.6.1) a ich veľkosť aj smer môžeme vyjadriť
rovnicami
sa určí podľa Archimedovho zákona. Táto sila je opačne orientovaná ako
tiažová sila, pôsobiaca na teleso pri pohybe v tekutine. Všetky tri sily ležia
v tej istej priamke (obr. 2.6.1) a ich veľkosť aj smer môžeme vyjadriť
rovnicami
![]()
![]()
![]()
v ktorých za kladný smer je považovaný smer tiažovej sily, m
je hmotnosť guľôčky, m´ je hmotnosť tekutiny s objemom rovným
objemu guľôčky, k je konštanta.
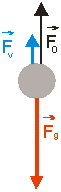
Obr. 2.6.1: Pohyb telesa v tekutine.
Výslednica
všetkých síl
![]() (2.6.1)
(2.6.1)
Vypočítame rýchlosť guľôčky, ktorá bola voľné pustená do tekutiny a
pohybuje sa vplyvom vyššie spomenutých síl. Pomocou vzťahu (2.6.1)
a jednej z rovníc pohybového zákona (2.2.2) dostaneme pohybovú
rovnicu (druhý typ 2. možnosť),
![]() , (2.6.2)
, (2.6.2)
úpravou
![]() (2.6.3)
(2.6.3)
v ktorej pomocou
![]() sme označili rozdiel hmotnosti.
sme označili rozdiel hmotnosti.
Rovnica
(2.6.3)
je diferenciálnou rovnicou
1. radu a môžeme ju upraviť na tvar
![]()
pričom
![]() .
.
Po
jednoduchej úprave
![]()
a integráciou
![]()
Integračnú
konštantu C určíme
z podmienky,
že v čase t = 0 s guľôčka bola v pokoji a teda rýchlosť v tomto okamihu v = 0 m/s.
Po dosadení týchto
hodnôt do predchádzajúcej rovnice
![]()
pre integračnú konštantu vyplýva vzťah
![]()
Po ďalšej úprave pre rýchlosť
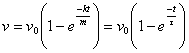
Vidíme,
že odvodená závislosť rýchlosti od času v porovnaní so závislosťou pre rýchlosť pri voľnom páde
![]() , keď na teleso pôsobí len
tiažová sila, má zložitejší priebeh
(modrá krivka obr. 2.6.2).
, keď na teleso pôsobí len
tiažová sila, má zložitejší priebeh
(modrá krivka obr. 2.6.2).
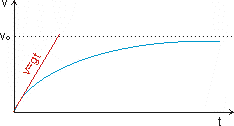
Obr. 2.6.2: Závislosť
rýchlosti guľôčky pri pohybe vo viskóznej tekutine od času.
Rýchlosť
exponenciálne narastá a teoreticky
v nekonečne veľkom čase nadobúda medznú hodnotu
![]() .
.
Z rovnice (2.6.1) vyplýva, že guľôčka nadobúda túto
rýchlosť v okamihu, keď výslednica všetkých síl F = 0.![]() .
.
Ľahko sa môžeme presvedčiť, že po čase
![]() hodnota rýchlosti je
hodnota rýchlosti je
![]() . Teda , už po relatívne krátkom čase
rýchlosť je prakticky konštantná a rovná hodnote medznej rýchlosti v0. Od uvedeného okamihu guľôčka v tekutine vykonáva rovnomerný
priamočiary pohyb (rýchlosť je daná červenou krivkou na obr. 2.6.2).
. Teda , už po relatívne krátkom čase
rýchlosť je prakticky konštantná a rovná hodnote medznej rýchlosti v0. Od uvedeného okamihu guľôčka v tekutine vykonáva rovnomerný
priamočiary pohyb (rýchlosť je daná červenou krivkou na obr. 2.6.2).
Tento poznatok je možné využiť pri skúmaní vlastnosti tekutín, napríklad pri určovaní viskozity tekutín pomocou Stokesovho telieskového viskozimetra. Je to nádoba tvaru valca dĺžky 1,2 m a polomeru 4 cm (obr. 2.6.3), do ktorej sú postupne vhadzované guľôčky z rovnakého materiálu a rovnakých vlastností (hmotnosť, polomer).
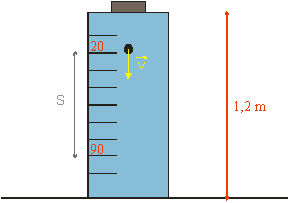
Obr.2.6.3: Stokesov telieskový viskozimeter.
V nádobe sa nachádza tekutina známej
hustoty, ktorej viskozitu chceme určiť. Pri pohybe guľôčky sa využíva poznatok,
že guľôčka sa po krátkom čase pohybuje rovnomerným priamočiarym pohybom
(v0 = konš.). Na zvolenom úseku (20 cm - 90 cm) sa zistí
doba, za ktorú tento úsek guľôčka prejde. Pomocou známej dráhy a doby sa
určí rýchlosť padajúcej guľôčky (v = s / t).
Viskozita v takomto prípade je daná vzťahom
![]() ,
,
kde r, v, r sú polomer, rýchlosť a
hustota materiálu guľôčky a rt
je hustota kvapaliny.