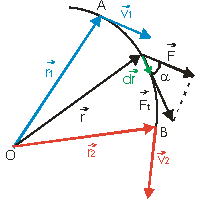
Obr. 2.3.1: Na hmotný bod pôsobí sila po dráhe, ktorá je určená bodmi A a B.
| 2.3 Hodnotenie účinkov sily a energia | Mechanická práca 1/9 |
Mechanická práca
K pojmu práce ako dráhového účinku sily sme vedení skúsenosťou,
napr. pri posúvaní bremena po dráhe. Práca sa tu koná tak, že sila posúva bremeno vo svojom smere po dráhe. A ak
sila a dráha majú rovnaký smer, zo strednej školy vieme, že prácu
potom definujeme ako súčin sily a dráhy (W = Fs). Ale
ako budeme definovať prácu, ak sa bude meniť veľkosť sily alebo ak sila a
dráha budú mať rôzny smer?
Majme hmotný bod, ktorý sa pohybuje po ľubovoľnej trajektórii (obr. 2.3.1). Zaujíma nás aký bude dráhový účinok sily, ktorá začne pôsobiť na hmotný bod na určitom zvolenom úseku trajektórie (medzi bodmi A a B).

Obr. 2.3.1: Na hmotný bod pôsobí sila po dráhe, ktorá je určená bodmi
A a B.
Polohy bodov A, B popíšme pomocou polohových vektorov
![]() vzhľadom na zvolený referenčný bod O a nech rýchlosti hmotného bodu v týchto bodoch sú
vzhľadom na zvolený referenčný bod O a nech rýchlosti hmotného bodu v týchto bodoch sú
![]() .
.
Dráhový účinok sily potom hodnotíme pomocou dráhového integrálu
sily
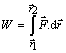 (2.3.1)
(2.3.1)
kde![]() je sila pôsobiaca na hmotný bod a
je sila pôsobiaca na hmotný bod a ![]() je
elementárne posunutie hmotného bodu. Skalárna veličina
W definovaná dráhovým integrálom (2.3.1) sa nazýva mechanická práca.
je
elementárne posunutie hmotného bodu. Skalárna veličina
W definovaná dráhovým integrálom (2.3.1) sa nazýva mechanická práca.
Vzťah
pre prácu môžme vyjadriť aj pomocou integrálu
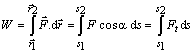 (2.3.2)
(2.3.2)
kde a
je
uhol medzi vektorom sily a elementárnym posunutím,
Ft
je veľkosť priemetu sily
do smeru pohybu pôsobiska sily v danom mieste dráhy a ds
je veľkosť elementárneho
posunutia hmotného bodu (obr. 2.3.1). Teda práca je určená dráhovým integrálom
priemetu sily do smeru pohybu pôsobiska sily.

|
Pri matematických úpravách vzťahu (2.3.2)
sme použili skalárny súčin vektorov
|
Zo vzťahov (2.3.1) a (2.3.2) vyplýva, že veľkosť práce závisí od veľkosti
sily, dráhy a od orientácie sily vzhľadom k smeru pohybu hmotného
bodu (možnosti výpočtu práce z
tohto hľadiska).
Kontrolka:
Obrázok znázorňuje tri prípady pôsobenia sily na hranol po hladkej podložke.
Pomocou vzťahu (2.3.2) zistite, ktorá z nich znázorňuje pôsobenie sily,
ktorej práca bude nulová.
|
|
|
|