Pohybová rovnica
Mechanický pohyb hmotného bodu môžeme skúmať pomocou základného pohybového zákona dynamiky - pohybovej rovnice. Jej vektorový tvar (berieme do úvahy aj smer jednotlivých vektorových veličín) v rámci klasickej fyziky vyplýva z druhého Newtonovho pohybového zákona
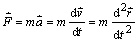      (2.2.1)

kde 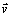, , 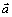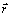sú vektor rýchlosti, zrýchlenia a polohového vektora (posunutia) hmotného bodu. 

Vo vzťahu (2.2.1)  je zrýchlenie 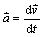 a rýchlosť 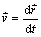 potom úpravou .

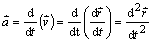Ak tento pohyb budeme vzťahovať k počiatku pravouhlého súradnicového systému potom môžme vektorový tvar pohybovej rovnice nahradiť troma skalárnymi pohybovými rovnicami (uvažujeme len veľkosti jednotlivých vektorových veličín) v tvare
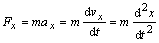  (2.2.2a)
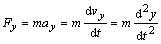  (2.2.2b)
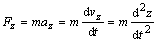   (2.2.2c)

 kde F_x , F_y , F_z , a_x , a_y , a_z , v_x , v_y , v_z sú súradnice sily, zrýchlenia a rýchlosti a x, y, z sú súradnice polohy hmotného bodu.

Ak sa hmotný bod pohybuje po priamke, stačí použiť len jednu rovnicu (súradnicu, napr. Fx), ak pôjde o pohyb v rovine dve rovnice a všetky tri pre prípad pohybu v priestore.