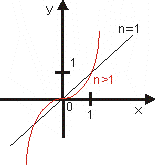Lineárna funkcia
Kvadratická funkcia
Nepriama úmernosť
Logaritmická funkcia
Exponenciálna funkcia
Mocninová funkcia
Goniometrická funkcia
Exponenciálna funkcia
Exponenciálnou funkciou so základom a sa nazýva každá
funkcia na množine R daná rovnicou: y = ax,
kde
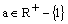 .
.
Grafom exponenciálnej funkcie je exponenciálna krivka.
Vlastnosti exponenciálnej funkcie sú uvedené v tabuľke Tab. 5 v závislosti od základu
a.
Funkcia y = ax
|
a > 1
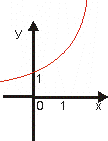
|
0 < a <
1 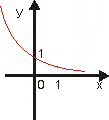
|
|
Definičný odbor je R |
|
Obor hodnôt je
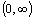 .
. |
|
Je rastúca a preto prostá. |
Je klesajúca a preto prostá. |
|
Je zdola ohraničená, nie je zhora ohraničená.
Nemá ani maximum ani minimum.
Funkčná hodnota v bode 0 sa rovná 1. |
Tab.5: Vlastnosti
exponenciálnej
funkcie.
Mocninová funkcia
Mocninová funkcia je každá funkcia daná rovnicou : y =
xn , kde
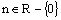 .
.
Vlastnosti mocninových funkcií závisia od exponenta n.
Prehľad udáva tabuľka.
1. y = xn,
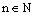 , n nepárne:
, n nepárne:
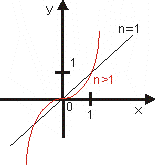
|
D (f) = R
H (f) = R
Je rastúca. Je nepárna.
Nie ani zhora
ani zdola ohraničená.
Nemá ani maximum ani minimum.
Napr.: y = x3, y = x5, ....
f (1) = 1 , f (-1) = - 1
|
| 2. y = xn, n párne:
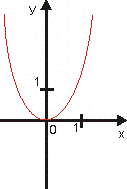
|
D(f) = R,
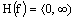
Je klesajúca na
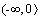 .
.
Je rastúca na
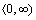 .
.
Je párna, zdola ohraničená.
Zhora nie je ohraničená.
V bode 0 má ostré minimum,
maximum nemá.
Napr: y = x2 , y = x4
, ... |
3. y = xn,
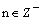 , n nepárne:
, n nepárne:
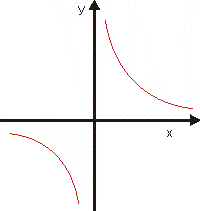
|
D (f) = H (f) =
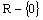
Je klesajúca na
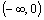 a
a
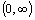 .
.
Nie je zhora, ani zdola ohraničená.
Je nepárna.
Nemá maximum ani minimum.
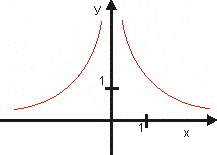
Napr: y = x-3
|
4. y = xn,
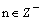 , n párne:
, n párne:
|
D(f) =
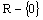
H(f) = R+
Rastie na
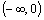 , klesá na
, klesá na
Je ohraničená zdola,
zhora nie je ohraničená.
Je párna.
Nemá maximum ani minimum.
Napr: y = x-2
|
5.
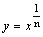
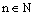 : :
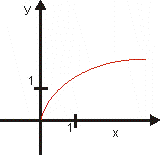
|
D (f) =
H (f) =
Rastúca na
Ohraničená zdola,
zhora neohraničená.
Má ostré minimum v bode x = 0.
Nemá maximum.
Napr: y = x1/2
|
Tab.6: Vlastnosti
mocninových funkcií.
Goniometrická funkcia
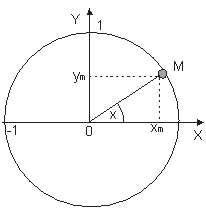
Jednotková kružnica je kružnica s polomerom 1, dĺžka takejto kružnice je 2p.
1 radián: Uhol ASB má veľkosť 1 radián (1 rad ) práve vtedy, keď sa
dĺžka oblúka AB rovná 1.
1 stupeň: Uhol ASC má veľkosť 1 stupeň (10) práve vtedy, keď má oblúk
AC dĺžku 2p : 360.
Dohoda: x - označenie čísel. hodnoty veľkosti uhla v oblúkovej miere,
a
- označenie čísel. hodnoty veľkosti uhla v stupňovej miere.
Platí:
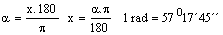
Definície funkcií:
Vlastnosti goniometrických funkcií
|
funkcie |
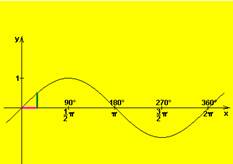
y = sin x |
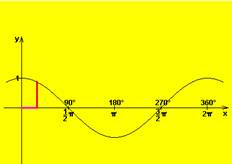
y = cos x |
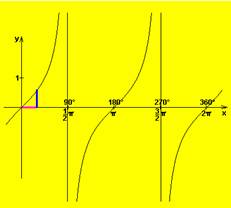
y = tg x |
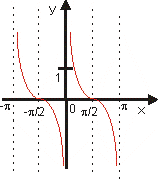
y = cotg x
|
|
definičný obor |
R |
R |
množina všetkých
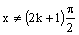
|
množina všetkých
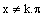
|
|
obor hodnôt |
<-1, 1> |
<-1, 1> |
R |
R |
|
rastúca |
na každom intervale
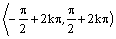
|
na každom intervale
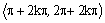
|
na každom intervale
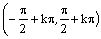
|
- |
|
klesajúca |
na každom intervale
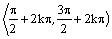
|
na každom intervale
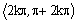
|
- |
na každom intervale
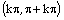
|
|
párnosť, nepárnosť |
nepárna |
párna |
nepárna |
nepárna |
|
ohraničenosť |
zhora i zdola ohraničená |
zhora i zdola ohraničená |
zhora ani zdola nie je ohraničená |
zhora ani zdola nie je ohraničená |
|
maximum |
v každom
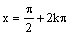
|
v každom
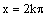
|
neexistuje |
neexistuje |
|
minimum |
v každom
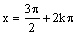
|
v každom
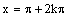
|
neexistuje |
neexistuje |
| a |
Znázornenie goniometrických
funkcií nájdete aj v aplete. |
Vlastnosti funkcií
Pre každé x, pre ktoré je funkcia
definovaná platí:
sin (-x) = - sin x
cos (-x) = cos x
tg (-x) = - tg x
cotg (-x) = - cotg x
Funkcia y = cos x je párna funkcia, ostatné sú nepárne.
Periodickosť funkcií.
Pre
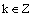 : sin (x +
2kp) = sin x
: sin (x +
2kp) = sin x
cos (x +
2kp) = cos x
Funkcie sínus a kosínus sú periodické a periódou 2p.
Pre x, pre ktoré sú tg x a cotg x definované:
tg (x +
kp) = tg x
cotg
(x +kp) = cotg x
Funkcie tangens a kotangens sú periodické s periódou p.
Hodnoty funkcií pre niektoré hodnoty uhla:
Vlastnosti funkcií - znamienka hodnôt funkcií:
| |
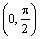
|
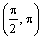
|
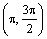
|
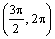
|
| (00, 90
0) |
(900, 180
0) |
(1800, 270
0) |
(2700, 360
0) |
| sin x |
+ |
+ |
- |
- |
| cos x |
+ |
- |
- |
+ |
| tg x |
+ |
- |
+ |
- |
| cotg x |
+ |
- |
+ |
- |