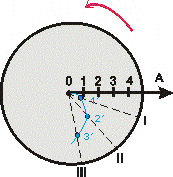
Príklad 2.1.1: Na os odstredivky pripevnime v horizontálnej rovine hladký disk a roztočíme ho (namiesto odstredivky môžme použiť aj gramofón). Zo stredu disku uvedieme do pohybu v smere polomeru guľku, natretú nevysýchajúcou farbou (obr. 2.1.5). Budeme pozorovať pohyb guľky dovtedy, kým guľka nespadne z disku, pričom nebudeme brať do úvahy trecie sily. Čo zistíme o pohybe guľky?

Riešenie: Keďže na guľku nepôsobia žiadne sily, guľka musí pokračovať v pohybe v smere polomeru po čiare OA. Tak to bude vyzerať, ak sa pozeráme na disk zhora. Keď guľka spadne z disku, zastavíme odstredivku a pozrieme sa, akú stopu zanechala guľka na povrchu disku. Guľka, na ktorú nepôsobia žiadne sily, nenakreslila priamku, ale špirálu. Z tohto vyplýva, že pre pozorovateľa spojeného s otáčajúcim sa diskom zákon zotrvačnosti neplatí. Vzhľadom na pozorovateľa v pokoji P, ktorý sa pozerá na disk zhora, sa guľka premiestňovala medzi bodmi 1, 2, 3. Pre pozorovateľa P´ spojeného s otáčajúcim sa diskom, sa guľka dostane do bodov 1´, 2´, 3´na polomeroch I, II, III. 

        

 Obr. 2.1.5: Dvaja pozorovatelia P a P´ pozorujú pohyb guľky, z dvoch rôznych vzťažných sústav.


Rozdielnosť pozorovaného pohybu guľky pozorovateľov P a P´ závisí od vzťažnej sústavy, v ktorej sa pozorovatelia nachádzajú. Keďže pozorovateľ P´ je spojený s otáčajúcim sa diskom, nachádza sa v neinerciálnej vzťažnej sústave. Pozorovateľ P je teda spojený s inerciálnou vzťažnou sústavou, ktorou je Zem.

Späť 


Príklad 2.1.2: Ak by sme sledovali hru hokeja na tom istom kotúči, ktorý je pripevnený na os odstredivky v horizontálnej rovine ako v predchádzajúcom príklade, z nášho pohľadu (pozorovateľ P´) bude vystrelený puk letieť po priamke s rýchlosťou v. Ako je možné, že to nie je krivka, keď v predchádzajúcom príklade to tak bolo? 

Riešenie: Ak predpokladáme, že uhlová rýchlosť Zeme je malá počas pohybu puku v smere polomeru kotúča, potom pozorujeme pohyb puku po priamke a nie po krivke. Teda predpokladáme, že v tomto prípade Zem predstavuje inerciálnu vzťažnú sústavu.

Späť


Príklad 2.1.3: Majme dva rovnaké valčeky z rôzneho materiálu, prvý je z hliníka a druhý z olova. Obidva sa pohybujú rovnakou rýchlosťou po hladkej podložke bez trenia. Akými veľkými silami máme na ne pôsobiť, aby sme ich zastavili  súčasne?

Riešenie: Keďže olovený valček má väčšiu hmotnosť ako hliníkový, má väčšiu schopnosť zotrvávať v svojom pohybovom stave. Teda na to, aby sme ich súčasne zastavili, musíme na ne pôsobiť rôzne veľkými silami, na olovený väčšou silou ako na hliníkový. Naopak, ak by sme chceli tieto valčeky uviesť do pohybového stavu, musíme opäť pôsobiť na olovený väčšou silou ako na hliníkový, pretože olovený valček má väčšiu schopnosť zotrvávať v pokoji.

Späť


Príklad 2.1.4: Čo bude ovplyvňovať rozdiel v pohybe valčekov v predchádzajúcom príklade?

Riešenie: Z predchádzajúceho príkladu vyplýva, že rozdiel v pohybe hliníkového a oloveného valčeka pri rovnakom polomeri, výške a rýchlosti bude určovať hybnosť oboch valčekov.

Späť


 Príklad 2.1.5: Pôsobením stálej sily 20 N prešlo teleso z pokoja za 10 s dráhu 25 m. Akú má hmotnosť?

 Riešenie: Zo zadania príkladu vyplýva, že sila pôsobiaca na teleso je konštantná. Potom na výpočet hmotnosti telesa použijeme vzťah (2.1.4) v skalárnom tvare, bez vektorov (keďže predpokladáme, že teleso sa pohybuje po priamke vplyvom pôsobenia sily)
.      (1)
Odtiaľ ďalej vyplýva, že teleso sa pohybuje s konštantným zrýchlením z pokoja v0 = 0, teda vykonáva rovnomerne zrýchlený priamočiary pohyb, ktorý vieme popísať rovnicami
    (2)
      (3)
Vyjadrením zrýchlenia z rovnice (2) a dosadením do rovnice (1) pre silu
,
 
odtiaľ pre hmotnosť 




Hmotnosť telesa je 40 kg.
 
 Ak by na teleso pôsobila sila, ktorá nie je konštantná, použili by sme pri výpočte vzťah (2.1.3) a iný postup výpočtu (vrátime sa k tomu v kapitole 2.2 Pohybová rovnica). Rovnicu (3) sme teraz pri výpočte nepoužili.

Späť