Riešenie: Vagón sa pohybuje priamočiaro so zrýchlením, preto vzťažná sústava spojená s vagónom bude neinerciálna. Na závažie pôsobí zotrvačná sila, ktorá má opačný smer ako zrýchlenie sústavy
Príklad 2.5.1:Vo vagóne je zavesené
závažie s hmotnosťou 200 g na niti dĺžky 1 m. O aký uhol
sa niť vychýli zo zvislej polohy, ak sa vagón bude pohybovať priamočiaro so zrýchlením
3m/s2?
Riešenie: Vagón sa pohybuje priamočiaro so zrýchlením,
preto vzťažná sústava spojená s vagónom bude neinerciálna. Na závažie pôsobí
zotrvačná sila, ktorá má opačný smer ako zrýchlenie sústavy
![]() . Okrem toho pôsobí závažie na niť svojou tiažou
. Okrem toho pôsobí závažie na niť svojou tiažou
![]() .Výslednica týchto síl bude kompenzovať účinok sily napínajúcej
niť
.Výslednica týchto síl bude kompenzovať účinok sily napínajúcej
niť
![]() , preto niť bude mať smer daný touto výslednicou síl
, preto niť bude mať smer daný touto výslednicou síl
![]() (obr. 2.5.6 ). Uhol,
o ktorý sa niť vychýli zo zvislej polohy potom
(obr. 2.5.6 ). Uhol,
o ktorý sa niť vychýli zo zvislej polohy potom
|
Dosadením veľkosti síl Fz = ma a G = mg do (1) úpravou a použitím číselných hodnôt Niť sa vychýli od zvislého smeru o 170. |
|
Príklad 2.5.2: Aká
je zdanlivá tiaž osoby hmotnosti 75 kg vo výťahu, ktorý sa
pohybuje
a) nahor spomalením 0,2 m/s2 a dolu so zrýchlením 0,2 m/s2
,
b) nahor so zrýchlením 0,15 m/s2 a dolu spomalením 0,15 m/s2.
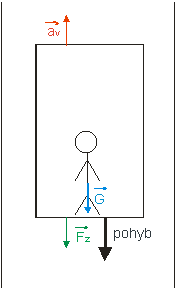
Riešenie: a) Výťah sa pohybuje smerom nahor so spomalením av a predstavuje neinerciálnu vzťažnú sústavu, preto na človeka pôsobí zotrvačná sila Fz, ktorá (má vždy opačný smer ako zrýchlenie sústavy) smeruje nahor (obr. 2.5.7a).
|
|
|
|
 |
|
a) |
b) |
c) |
d) |
Obr. 2.5.7
Potom zdanlivá tiaž človeka
je daná
![]() resp.
resp.
G´= G - Fz dosadením
G´=mg - mav
G´= 75.9,81 - 75.0,2 = 720,75 N
Ak porovnáme skutočnú tiaž človeka G = mg = 735,75 N,
ktorú má v prípade, keď sa výťah pohybuje s konštantnou rýchlosťou
alebo je v pokoji (av =
0) so zdanlivou tiažou G´ potom G > G´. Odtiaľ vyplýva,
že človek pociťuje vo výťahu odľahčenie. Tá istá situácia platí v prípade,
keď výťah sa pohybuje nadol zo zrýchlením (obr. 2.5.7b).
Zdanlivá tiaž človeka vo výťahu je 720,75 N.
Ak by sa výťah rozbiehal nadol voľným pádom (zrýchlenie výťahu av = g) potom by nastal bezťiažový stav, zdanlivá tiaž G´= G - Fz = mg - mav = mg - mg = 0.
b)V
prípade, že sa výťah pohybuje nahor so zrýchlením av
(obr. 2.5.7c) a nadol so spomalením (obr. 2.5.7d) na človeka pôsobí zotrvačná
sila smerom nadol (opačný smer ako av ). Potom
zdanlivá tiaž
G´= G + Fz dosadením
G´=mg + mav
G´= 75.9,81 + 75.0,2 = 747 N
Porovnaním
so skutočnou tiažou človeka G je G´ > G,
teda človek pociťuje vo výťahu preťaženie.
Zdanlivá tiaž človeka vo výťahu je 747 N.
Príklad 2.5.3: Automobil hmotnosti 1000 kg sa pohybuje po vydutom moste rýchlosťou 36 km/hod. Polomer krivosti v strede mosta je 50 m. Akou silou tlačí automobil na most v okamihu prechodu stredom mosta?
Riešenie:
Pri riešení
úlohy uvažujeme vzťažnú sústavu, ktorá je pevne spojená s autom. Auto
prechádza vydutým mostom, koná krivočiary (otáčavý) pohyb mení sa rýchlosť
auto, preto táto sústava je neinerciálna. Výsledná
sila, ktorou auto pôsobí na most je daná rozdielom tiaže auta a zotrvačnej
odstredivej sily, ktorá vznikla v dôsledku neinerciality sústavy (obr. 2.5.8)
|
F = G - F0 .
(1)
|
|
Príklad 2.5.4:
Na 450 zemepisnej šírky dopadá na zemský povrch rýchlosťou 100 m/s
teleso o hmotnosti 10 kg.
Aká je hodnota zotrvačnej odstredivej a Coriolisovej sily, ktoré na toto
teleso pôsobia, pri dopade na zemský povrch?
Riešenie: Pre hodnoty zotrvačnej odstredivej a Coriolisovej sily platia vzťahy:
![]() (1)
(1)
![]() (2)
(2)
 |
Na vyjadrenie Coriolisovej sily vo vzťahu (2) sme použili veľkosť vektorového súčinu. |
|
|
|
| a) | b) |
Obr. 2.5.9
Podľa
obr. 2.5.9a pre r platí
![]() , kde R je polomer Zeme, potom
, kde R je polomer Zeme, potom
![]() . Pre
. Pre
![]() , kde f je frekvencia otáčania Zeme, čo predstavuje
1 otáčku za 24 hodín (resp. 1 otáčku za 86400 sekúnd). Dosadením
, kde f je frekvencia otáčania Zeme, čo predstavuje
1 otáčku za 24 hodín (resp. 1 otáčku za 86400 sekúnd). Dosadením
![]()
![]()
Pre
uhol![]() (uhol medzi
(uhol medzi
![]() ) z
obr.2.5.9b platí
) z
obr.2.5.9b platí
![]() . Potom
. Potom
![]()
![]()
 |
Aby sme mohli zistiť uhol
|
Zotrvačná odstredivá sila pôsobiace na padajúce teleso je 0,238N a Coriolisova sila 1,028 N.