Silové pôsobenie v neinerciálnych sústavách - rotačný pohyb
V tejto časti si odpovieme na otázku, prečo pri jazde autom sa taška položená na sedadle auta pohne pri prudkom vjazde do zákruty alebo, keď prechádzame vo vlaku cez prudkú zákrutu, prečo máme dojem, že nás nejaká sila tlačí na vonkajšiu stenu vlaku? 

 Nech sústava S´ sa vzhľadom k sústave S otáča konštantnou uhlovou rýchlosťou tak, že počiatky týchto sústav sú totožné a osou otáčania je os Z´= Z (obr.2.5.4).

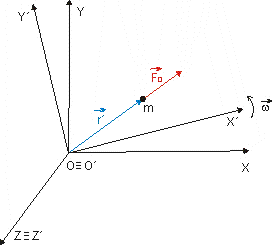
Obr. 2.5.4: Znázornenie neinerciálnej sústavy S´ rotujúcej vzhľadom k inerciálnej sústave S. Sústava S´ sa vzhľadom k  S otáča konštantnou uhlovou rýchlosťou w okolo osi Z´= Z.

Bez odvodenia uvedieme, že v uvedenom prípade silapôsobiaca na teleso, ktoré vzhľadom k sústave S´ je v pokoji sa vypočíta podľa vzťahu     
(2.5.8)

v ktorom je opäť skutočnou silou pôsobiacou na hmotný bod. 

Sily a sú  zdanlivé sily, ktoré  sa v rovnici  (2.6.8) objavili v dôsledku matematickej transformácie zákona sily z inerciálnej do uvažovanej neinerciálnej sústavy. Sila sa nazýva zotrvačná odstredivá sila a Coriolisova sila. Ak sústavu S´ zvolíme tak, že hmotný bod sa nachádza v rovine X´ Y´ potom vektor určuje polohu hmotného bodu vzhľadom k počiatku O = O´. 

Príklad 2.5.3

Odstredivá sila pôsobí na teleso v pokoji alebo v pohybe, Coriolisova sila pôsobí len na pohybujúce sa telesá.

Príklad 2.5.4

Dôsledky pôsobenia fiktívnych síl sú súčasťou nášho života, vplyvom rotácie Zeme. Niektoré z nich už boli spomenuté v predchádzajúcich kapitolách. Napríklad vplyvom zotrvačnej odstredivej sily sa na retiazkovom kolotoči rozostúpia sedadla o nejaký uhol a vzhľadom na os otáčania. Rovnaká sila má za dôsledok, že taška položená na sedadle auta sa pohne pri prudkom vjazde do zákruty tá istá sila spôsobuje, že pri prechádzaní vo vlaku cez prudkú zákrutu, máme dojem, že nás nejaká sila tlačí na vonkajšiu stenu vlaku.

Zemeguľa sa točí proti smeru pohybu hodinových ručičiek, ak sa na ňu pozeráme ,,zhora" na severný pól. Preto sa teleso pohybujúce pozdĺž zemského povrchu, musí na severnej pologuli odkláňať vpravo od smeru pohybu, vplyvom Coriolisovej sily. Toto platí rovnako aj pre pohyb po poludníku. Corilisova sila ovplyvňuje pohyb morských prúdov, smery vetrov, vymieľanie pravých brehov riek, opotrebovanie koľajníc, odklon striel zo zbraní, vytekanie vody z umývadla (pozri video na vytekanie vody z umývadla: http://sis.science.upjs.sk/fyzika/ucebnetexty/coriolis/index.html  v časti Kukni tu - Kde bolo tam bolo, aktuálne 20.7. 2007).

Vráťme sa k problému z úvodu tejto kapitoly, prečo vo Washingtone a Lisabone, ktoré ležia na jednej rovnobežke, je výrazne iné počasie, kým v Lisabone sa ľudia kúpu, tak vo Washingtone sneží? Vplyvom Coriolisovej sily významný teplý Golfský prúd, ktorý vzniká v Mexickom zálive sa stáča doprava k brehom Európy, prechádza popri Nórsku a otepľuje pobrežné vetry. Vďaka nemu sú zimné teploty v severozápadnej Európe o 11 ⁰C vyššie než priemerná teplota týchto šírok.  

Vplyv rotácie na veľkosť tiažového zrýchlenia
Príkladom neinerciálnych sústav tohto druhu môže byť sústava pevne spojená so Zemou. Na teleso o hmotnosti m, ktoré sa na zemskom povrchu nachádza v pokoji pôsobí gravitačná sila . Z hľadiska sústavy spojenej so Zemou pôsobí okrem gravitačnej sily, ktorá smeruje do stredu Zeme, aj  zotrvačná odstredivá sila , ktorá je omnoho menšia ako gravitačná sila a je orientovaná v smere od osi rotácie Zeme (obr.2.6.5).

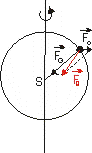
Obr. 2.5.5: Z hľadiska neinerciálnej sústavy S´ pôsobí na teleso, ktoré je na zemskom povrchu v pokoji, okrem gravitačnej sily F_G aj zotrvačná odstredivá sila F_o.

Výslednica týchto dvoch síl má veľkosť, ktorá je nepatrne odlišná od veľkosti gravitačnej sily a je mierne odchýlená od smeru gravitačnej sily. Výslednica gravitačnej a zotrvačnej sily sa nazýva tiažová sila .

Tiažová sila a tiažové zrýchlenie sa menia v závislosti od zemepisnej šírky a nadmorskej výšky. Existuje tzv. Hayfordov vzťah  pre výpočet miestneho tiažového zrýchlenia v tvare

 

kde b je zemepisná šírka a h je nadmorská výška. 

Pre Katedru fyziky v Košiciach má miestne tiažové zrýchlenie hodnotu g = 9,808565367 m/s² pričom b = 48⁰ 43´´ a h = 220 m. V našich podmienkach sa pri výpočte tiažovej sily používa hodnota pre normálne tiažové zrýchlenie g = 9,81 ms^-2. Na póloch má tiažové zrýchlenie hodnotu 9,832 ms^-2 a na rovníku 9,78 ms^-2.