Príklad 2.4.1:Vypočítajte,
koľkokrát je tiažové zrýchlenie na Mesiaci menšie ako tiažové zrýchlenie
na Zemi, ak tiažová sila pôsobiaca na padajúcu skalu na Mesiaci má
hodnotu 11,445 N a na Zemi 68,67 N. Aká je hodnota
tiažového zrýchlenia na Mesiaci a aká
je hmotnosť skaly na Mesiaci a na Zemi?
Riešenie: Označme Fgm= 11,445 N tiažovú silu pôsobiacu na padajúcu
skalu na
Mesiaci a tiažové zrýchlenie gm
a analogický Fgz=
68,67 N tiažovú silu na Zemi a tiažové zrýchlenie gz.
a) Zaujíma nás, koľkokrát je tiažové zrýchlenie na Mesiaci menšie ako
tiažové zrýchlenie na Zemi, teda podiel
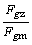 (1).
(1).
Podľa vzťahu (2.4.1)
veľkosť oboch tiažových síl môžme vyjadriť v tvare
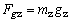
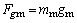 (2),
(2),
keďže hmotnosť skaly
je charakteristikou samotného predmetu, bude jej hodnota rovnaká v ktoromkoľvek
mieste, aj na Zemi aj na
Mesiaci, teda
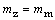 .
Potom po dosadení vzťahov (2) a za hmotnosť do vzťahu
(1)
.
Potom po dosadení vzťahov (2) a za hmotnosť do vzťahu
(1)
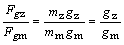
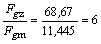
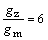 (3)
(3)
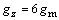
Tiažové zrýchlenie pôsobiace na padajúcu skalu na Mesiaci je 6 - krát menšie ako
tiažové zrýchlenie na Zemi.
b) Hodnotu tiažového
zrýchlenia na Mesiaci vypočítame priamo zo vzťahu (3), ktorý sme odvodili v predchádzajúcom
výpočte, kde uvažujeme hodnotu gz = 9,81 m/s2. Úpravou pre tiažové
zrýchlenie na Mesiaci
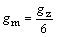
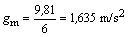
Hodnota tiažového zrýchlenia
na Mesiaci je 1,635 m/s2.
c) V časti
a) tohto príkladu sme predpokladali, že hmotnosť medicinbalu je rovnaká vzhľadom
na Zem aj Mesiac. Použitím niektorého zo vzťahov (2) pre výpočet hmotnosti
dostávame
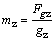
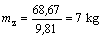
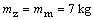
Hmotnosť medicinbalu na Zemi aj na Mesiaci je 7 kg.
Späť
Príklad 2.4.2: Medzi zaujímavé zimné športy
určite patrí jazda na boboch. Veľká rýchlosť množstvo zákrut, najrýchlejšie
vyštartovanie a nasadnutie do bobov, to všetko robí tento šport príťažlivým
pre divákov. Ale je tento šport aj bezpečný? Aké nároky sú kladené na
fyzickú a psychickú kondíciu bobistov? Vypočítajte akému preťaženiu je
vystavený bobista prechádzajúci plnou rýchlosťou zákrutu bobovej dráhy?
Predpokladajme, že bobista s hmotnosťou 80 kg dosahuje v zákrute o
polomere 20 m rýchlosť 100 km/hod.
Riešenie: Pri
jazde na boboch sa uplatňuje pôsobenie dostredivej sily, čo sa prejaví ako
tzv. preťaženie (spôsobuje bobistovi pocit ,,oťaženia“), ktorého veľkosť
závisí od dostredivej sily. Pri výpočte budeme postupovať tak, že vypočítame
veľkosť dostredivej sily (je ňou normálová zložka sily) (1), ktorá pôsobí v zákrute na bobistu a aj veľkosť
tiaže (2) bobistu v tejto zákrute. Pre dostredivú silu
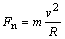 (1)
(1)
a pre tiaž
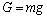 (2)
(2)
Ich podielom (3) získame hodnotu preťaženia bobistu v zákrute:
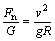 (3)
(3)
a po číselnom dosadení
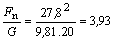
Bobista
má pocit, že v zákrute takmer 4 - krát ,,oťažel".
Odborníci z oblasti letectva
majú zistené, aký vplyv na ľudský organizmus majú veľké dostredivé
sily, ktoré vznikajú vzhľadom na veľké rýchlosti a zmeny smeru pohybu. Pri
preťažení, ktoré sa rovná 2g človeka a trvajúcom
2 s pociťuje človek sťaženie dýchanie a pohyby končatín.
Pri preťažení 4g poruchy zraku a pri preťažení 5g
nebezpečenstvo
straty vedomia. Preto v letectve existujú normy,
ktoré určujú akú ,, ostrú zákrutu“ si pilot môže dovoliť.
Z nášho výsledku vyplýva, že bobista musí znášať v zákrutách (ktoré
tvoria asi 1/3 trate, je ich 10 – 15 na 1100 – 1500 metrovej trati) pomerne
veľké preťaženie nehovoriac o ďalších nárokoch, ktoré sú naňho
kladené (sila a rýchlosť pri štarte, nároky na schopnosť sa
orientovať na trati a zvládnuť rýchlosť).
Späť
Príklad
2.4.3: Kamenný kváder je ťahaný rovnomerným pohybom
po vodorovnej rovine ťahovou silou traktora F = 2,1.103
N.
a) Aká je veľká tiaž kvádra, ak faktor šmykového
trenia medzi kvádrom a rovinou je µ = 0,7?
b) Utiahne traktor o tiaži G´= 20.103 N kamenný
kváder, ak jeho kolesá vojdú do
zablatenej cesty, kde faktor šmykového trenia medzi kolesami traktora
a cestou je µ´ =
0,12?
Riešenie:
a)
Pri rovnomernom pohybe je ťahová
sila traktora F v rovnováhe s trecou silou Ft
, pričom Ft = µFn
(1) a
normálová
sila Fn je sila kolmá na podložku. V tomto prípade je daná
tiažou kvádra Fn = G (2),
potom ťahová sila traktora
F = Ft
.
Dosadením (1) a (2) do tejto rovnice
F = µG.
Pre tiaž kamenného kvádra
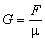
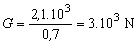
Tiaž
kvádra je 3.10 3 N.
b) Ak
má traktor tiaže G´ utiahnuť kváder
aj vtedy, keď vojdú jeho kolesá na zablatenú cestu, musí
trecia sila Ft´ vznikajúca medzi pneumatikami kolies
a cestou byť väčšia ako ťahová sila F
potrebná k udržaniu pohybu kvádra. Musí teda platiť
Ft´
>
F.
Na vyjadrenie trecej sily použijeme vzťah (1), kde za Fn = G´,
potom
Ft´ = µ´G´
Ft´ = 0,12.20.103 = 2,4.103 N
Keďže Ft´ >
F = 2,1.10 3 N, trecia sila
k pohybu traktora ešte postačuje.
Späť
Príklad 2.4.4:
Kváder o hmotnosti 10 kg leží na
vodorovnej rovine. Akou veľkou vodorovnou silou
F musíme na neho pôsobiť, aby za
dobu 2 s nadobudol rýchlosť 3 m/s
a) bez trenia
b)
ak faktor šmykového trenia µ = 0,1.
Kváder
sa pohybuje rovnomerne zrýchleným priamočiarym pohybom.
Riešenie: a) Vodorovnú silu, ktorou máme pôsobiť na
kváder vyjadríme v tvare F = ma (1). Zo zadania
vyplýva, že kváder vykonáva rovnomerne zrýchlený priamočiary pohyb, ktorého
rýchlosť vieme vyjadriť v = v0 + at
(2). Kváder je na začiatku pohybu v pokoji, preto v0 = 0 m/s.
Vyjadrením zrýchlenia z rovnice (2) a dosadením do rovnice (1) vodorovná
sila
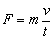
a dosadením
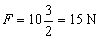
Na
kváder musíme pôsobiť silou 15 N, ak trenie zanedbávame.
b) Ak berieme do úvahy vplyv trecej sily na pohyb kvádra, potom na kváder
pôsobí okrem našej vodorovnej sily F aj trecia sila Ft,
ktorá pôsobí proti pohybu kvádra. Výsledná sila, ktorá pôsobí na kváder
je F´ = F - Ft
(3). Odtiaľ pre vodorovnú silu F = F´ + Ft,
kde F´ = ma (4) a Ft = µFn
(5). Normálová sila Fn je daná tiažou kvádra G = mg (6). Dosadením vzťahov
(4) - (6) do vzťahu (3) vodorovná sila, ktorou máme pôsobiť na kváder
je
F = ma + µmg.
Zo vzťahu (2) pre zrýchlenie
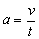 pri zohľadnení podmienky v0 = 0 m/s.
Dosadením
pri zohľadnení podmienky v0 = 0 m/s.
Dosadením
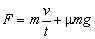
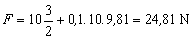
Na kváder musíme pôsobiť silou väčšou ako v prvom
prípade a to silou približne 25 N.
Späť
Príklad 2.4.5: Určte odporovú silu, ktorá pôsobí
na ponorku pod vodou pri rýchlosti 4
m/s, ak má ponorka prierez s obsahom 15 m2 a
faktor
odporu je C = 0,03.
(Hustota vody je 1000 kg/m3).
Riešenie: Na výpočet veľkosti odporovej sily použijeme vzťah
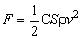
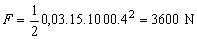
Odporová sila vody , ktorá pôsobí
na ponorku je 3,6 kN .
Späť