Silové pôsobenie v inercialných sústavách
Uvažujme o dvoch sústavách S a S´,
v ktorých sústava
S´ sa vzhľadom k S pohybuje tak, že osi týchto sústav sú
stále rovnobežné
(sústavy sa vzhľadom k sebe neotáčajú) a ich počiatky O a
O´ boli v čase t´=
0 totožné. Poloha sústavy S´ voči
S nech je určená vektorom
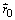 . Predpokladajme, že sústava S´
sa voči sústave S, pohybuje rýchlosťou
. Predpokladajme, že sústava S´
sa voči sústave S, pohybuje rýchlosťou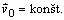 (obr.
2.5.2). Zaujíma nás, aké je silové pôsobenie v sústavách na
hmotný bod, teda aké je zrýchlenie v týchto sústavách.
(obr.
2.5.2). Zaujíma nás, aké je silové pôsobenie v sústavách na
hmotný bod, teda aké je zrýchlenie v týchto sústavách.
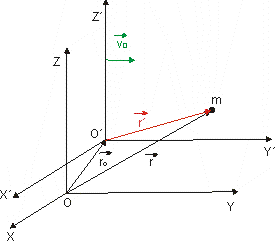
Obr. 2.5.2: Sústava
S´ sa vzhľadom k sústave S pohybuje s konštantnou rýchlosťou v0
tak, že osi obidvoch sústav sú stále rovnobežné a ich počiatky boli na začiatku
totožné.
Pre sústavy platí veta o skladaní rýchlosti
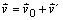
deriváciou ktorej podľa času
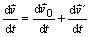 . (2.5.3)
. (2.5.3)
V takom prípade zrýchlenie
hmotného bodu v sústave S je rovnaké ako v sústave
S´ a naopak, t.j.
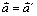 .
(2.5.4)
.
(2.5.4)
 |
Vo vzťahu (2.5.4) člen
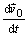 vypadne, pretože
vypadne, pretože
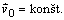 a
a
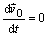 .
. |
Z poslednej rovnice vyplýva, že vo všetkých
vzťažných sústavách, ktoré
sa voči sebe nachádzajú v rovnomernom priamočiarom pohybe, zrýchlenie
pohybujúceho sa telesa je rovnaké. Z uvedeného rozboru vyplýva a aj to experimenty potvrdzujú, že sily pôsobiace na telesá sú nezávislé
od voľby inerciálnej vzťažnej sústavy a pohybový zákon (2.1.2)
má rovnaký
tvar vo všetkých inercialných sústavách. Iná situácia sa však pozoruje,
ak sústavy nie sú inerciálne.
Kontrolka:
Vyberte správnu odpoveď. Ak sa sústavy S´a S
voči sebe pohybujú s rýchlosťou, ktorá sa mení s časom (
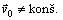 ) pričom platí, že osi týchto sústav sú
stále rovnobežné (sústavy sa vzhľadom k sebe neotáčajú) a ich počiatky O a
O´ boli v čase t´=
0 totožné, bude zrýchlenie v obidvoch sústavách: a) nulové, b) rovnaké, c)
rôzne.
) pričom platí, že osi týchto sústav sú
stále rovnobežné (sústavy sa vzhľadom k sebe neotáčajú) a ich počiatky O a
O´ boli v čase t´=
0 totožné, bude zrýchlenie v obidvoch sústavách: a) nulové, b) rovnaké, c)
rôzne.

