Neurčitý integrál
Vlastnosti neurčitého integrálu
Prehľad neurčitých integrálov základných funkcií
Určitý integrál
Aplikácie určitého integrálu
Vlastnosti určitého integrálu

Neurčitý integrál
Primitívna funkcia.  Nech f  je funkcia, . Funkciu F nazveme primitívnou k funkcii f na (a, b), ak  F´(x) = f (x) pre .

Neurčitý integrál. Ľubovoľnú z primitívnych funkcií k funkcii f nazývame neurčitým integrálom a zapisujeme: .

Vlastnosti neurčitého integrálu:  
Ak F je primitívna funkcia k f a G je primitívna funkcia ku g  na (a, b), tak :
1.

2.

3.

4.  funkcia y = c₁ . F (x) + c₂ . G (x) je primitívna k funkcii  y = c₁ . f (x) + c₂ . g (x) na (a, b).

Prehľad neurčitých integrálov základných funkcií:

Funkcia	Podmienky
	pre každé a
	pre každé
	pre
	pre
	pre
	pre
	pre
	pre
	pre
	pre

Určitý integrál
Určitý integrál. Nech f je spojitá v každom bode  < a, b >. Číslo I nazývame určitým integrálom od a po b z funkcie f a označujeme .


Newton - Leibnitzova formula: F(x)  je primitívna funkcia k f (x).

Aplikácie určitého integrálu:
 - g e o  m e t r i c k é - výpočet obsahu rovinných útvarov, objemu rotačných telies, dĺžky krivky, povrchu rotačnej plochy,...
 - f y z i k á l n e - uvádzame najjednoduchšie:

Príklad 1: Ak veľkosť rýchlosti hmotného bodu je funkcia  v = f(t), tak jeho dráhu v čase od t_z do t_k vypočítame:


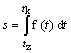
Príklad 2: Ak sa hmotný bod pohybuje po priamke a veľkosť sily závisí od súradnice x podľa vzťahu  F = f(x), tak pre výpočet práce na dráhe  <a, b>  platí:

Vlastnosti určitého integrálu. Nech f je spojitá funkcia na <a, b>.